Crossed ladders problem

The problem

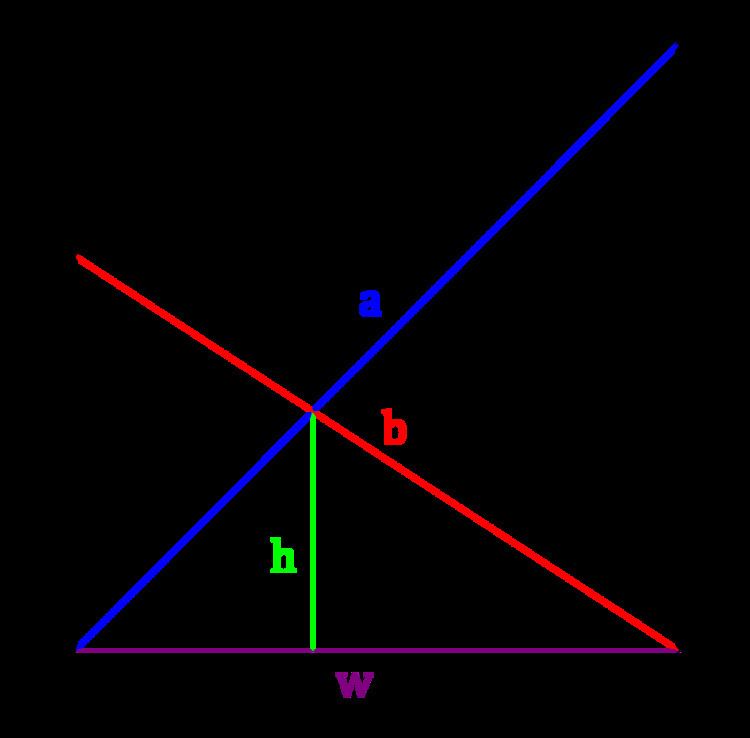
Two ladders of lengths a and b lie oppositely across an alley, as shown in the figure. The ladders cross at a height of h above the alley floor. What is the width of the alley?

Martin Gardner presents and discusses the problem in his book of mathematical puzzles published in 1979 and cites references to it as early as 1895. The crossed ladders problem may appear in various forms, with variations in name, using various lengths and heights, or requesting unusual solutions such as cases where all values are integers. Its charm has been attributed to a seeming simplicity which can quickly devolve into an “algebraic mess” (characterization attributed by Gardner to D. F. Church).

Solution

The problem description implies that w > 0, that a > w, and b > w, that h > 0, and that A > h, B > h, where A and B are the heights of the walls where sides of lengths b and a respectively lean (as in the above graph).

Both solution methods below rely on the property that 1 A + 1 B = 1 h , which can be seen as follows:

Divide the baseline into two parts at the point where it meets h , and call the left and right parts w 1 and w 2 , respectively. The angle where a meets w is common to two similar triangles with bases w and w 1 respectively. The angle where b meets w is common to two similar triangles with bases w and w 2 respectively. This tells us thatwhich we can then re-arrange (using w 1 + w 2 = w ) to get

First method

Two statements of the Pythagorean theorem (see figure above)

andcan be subtracted one from the other to eliminate w, and the result can be combined with 1 A + 1 B = 1 h with alternately A or B solved out to yield the quartic equationsThese can be solved algebraically or numerically for the wall heights A and B, and the Pythagorean theorem on one of the triangles can be used to solve for the width w.

Second method

The problem may be reduced to the quartic equation x ³(x − c) − 1 = 0, which can be solved by approximation methods, as suggested by Gardner, or the quartic may be solved in closed form by Ferrari's method. Once x is obtained, the width of the alley is readily calculated. A derivation of the quartic is given below, along with the desired width in terms of the quartic solution. Note that the requested unknown, w, does not appear directly in most of the derivation.

From 1 A + 1 B = 1 h , we getUsing the Pythagorean theorem, we can see thatBy isolating w² on both equations, we see thatwhich can be rearranged and factored intoSquare (Eq 2) and combine with (Eq 1)Rearrange to getThenNow, combine with (Eq 1)FinallyLetThenThe above fourth power equation can be solved for x using any available method. The width of the alley is then found by using the value found for x: The identity A + B = A + A 2 + ( a 2 − b 2 ) can be used to find A, and w can finally be found by w = b 2 − A 2 .

A quartic equation has four solutions, and only one solution for this equation matches the problem as presented. Another solution is for a case where one ladder (and wall) is below ground level and the other above ground level. In this case the ladders do not actually cross, but their extensions do so at the specified height. The other two solutions are a pair of conjugate complex numbers. The equation does not have the ladder lengths explicitly defined, only the difference of their squares, so one could take the length as any value that makes them cross, and the wall spacing would be defined as between where the ladders intersect the walls.

As the wall separation approaches zero, the height of the crossing approaches h = a b a + b . This is because 1 A + 1 B = 1 h (proven at the start) implies h = A B A + B , and as w goes to zero b goes to A and a goes to B according to the top diagram.

As the solutions to the equation involve square roots, negative roots are equally valid. They can be interpreted as both ladders and walls being below ground level and with them in opposing sense, they can be interchanged.

The complex solutions can be interpreted as wall A leaning to the left or right and wall B below ground, so the intersection is between extensions to the ladders as shown for the case {{{1}}} The ladders a and b and a 2 − b 2 are not as specified. The base w is a function of A, B, and h and the complex values of A and B can be found from the alternative quartic

x 4 − 2 h x 3 + D x 2 − 2 h D x + h 2 D = 0

with D being a 2 − b 2 for one wall and b 2 − a 2 for the other (±5 in the example). Note that the imaginary solutions are horizontal and the real ones are vertical. The value D is found in the solution as the real part of the difference in the squares of the complex coordinates of the two walls. The imaginary part = 2X_aY_a = 2X_bY_b (walls a and b). The short ladder in the complex solution in the 3,2,1 case appears to be tilted at 45 degrees, but actually slightly less with a tangent of 0.993. Other combinations of ladder lengths and crossover height have comparable complex solutions. With combination 105,87,35 the short ladder tangent is approximately 0.75.

Integer solutions

There are solutions in which all parameters are integers—for example, (a, b, A, B, w₁, w₂, w, h) = (119, 70, 42, 105, 16, 40, 56, 30). Such solutions involve Pythagorean triples for the two right triangles with sides (A, w, b) and (B, w, a) and integer solutions of the optic equation 1 A + 1 B = 1 h .