Multidimensional sampling

Preliminaries

The concept of a bandlimited function in one dimension can be generalized to the notion of a wavenumber-limited function in higher dimensions. Recall that the Fourier transform of an integrable function f ( ⋅ ) on n-dimensional Euclidean space is defined as:

where x and ξ are n-dimensional vectors, and ⟨ x , ξ ⟩ is the inner product of the vectors. The function f ( ⋅ ) is said to be wavenumber-limited to a set Ω if the Fourier transform satisfies f ^ ( ξ ) = 0 for ξ ∉ Ω .

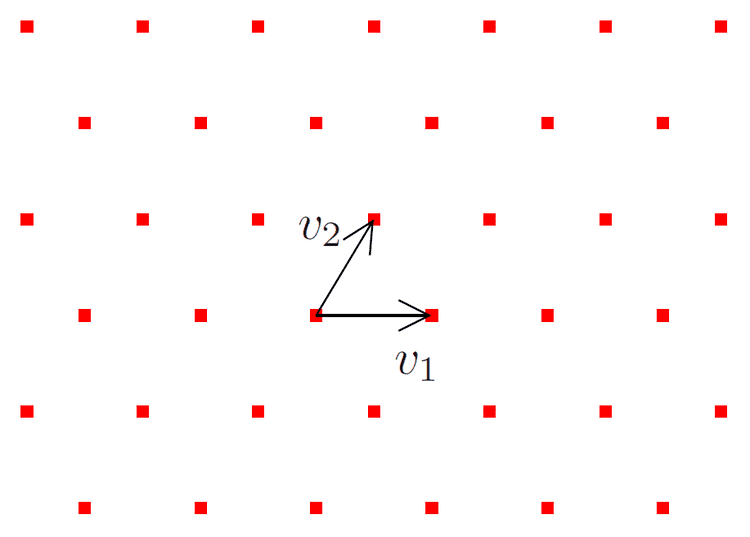
Similarly, the configuration of uniformly spaced sampling points in one-dimension can be generalized to a lattice in higher dimensions. A lattice is a collection of points Λ ⊂ ℜ n of the form Λ = { ∑ i = 1 n a i v i | a i ∈ Z } where {v₁, ..., v_n} is a basis for ℜ n . The reciprocal lattice Γ corresponding to Λ is defined by

where the vectors u i are chosen to satisfy ⟨ u i , v j ⟩ = δ i j . That is, if the vectors u i form columns of a matrix A and v i the columns of a matrix B , then A = B − T . An example of a sampling lattice in two dimensional space is a hexagonal lattice depicted in Figure 1. The corresponding reciprocal lattice is shown in Figure 2. The reciprocal lattice of a square lattice in two dimensions is another square lattice. In three dimensional space the reciprocal lattice of a face-centered cubic (FCC) lattice is a hexagonal close-packed (HCP) lattice or a body centered cubic (BCC) lattice.

The theorem

Let Λ denote a lattice in ℜ n and Γ the corresponding reciprocal lattice. The theorem of Petersen and Middleton states that a function f ( ⋅ ) that is wavenumber-limited to a set Ω ⊂ ℜ n can be exactly reconstructed from its measurements on Λ provided that the set Ω does not overlap with any of its shifted versions Ω + x where the shift x is any nonzero element of the reciprocal lattice Γ . In other words, f ( ⋅ ) can be exactly reconstructed from its measurements on Λ provided that Ω ∩ { x + y : y ∈ Ω } = ϕ for all x ∈ Γ ∖ { 0 } .

Reconstruction

The generalization of the Poisson summation formula to higher dimensions can be used to show that the samples, { f ( x ) : x ∈ Λ } , of the function f ( ⋅ ) on the lattice Λ are sufficient to create a periodic summation of the function f ^ ( ⋅ ) . The result is:

where | Λ | represents the volume of the parallelepiped formed by the vectors {v₁, ..., v_n}. This periodic function is often referred to as the sampled spectrum and can be interpreted as the analogue of the discrete-time Fourier transform (DTFT) in higher dimensions. If the original wavenumber-limited spectrum f ^ ( ⋅ ) is supported on the set Ω then the function f ^ s ( ⋅ ) is supported on periodic repetitions of Ω shifted by points on the reciprocal lattice Γ . If the conditions of the Petersen-Middleton theorem are met, then the function f ^ s ( ξ ) is equal to f ^ ( ξ ) for all ξ ∈ Ω , and hence the original field can be exactly reconstructed from the samples. In this case the reconstructed field matches the original field and can be expressed in terms of the samples as

where χ ˇ Ω ( ⋅ ) is the inverse Fourier transform of the characteristic function of the set Ω . This interpolation formula is the higher-dimensional equivalent of the Whittaker–Shannon interpolation formula.

As an example suppose that Ω is a circular disc. Figure 3 illustrates the support of f ^ s ( ⋅ ) when the conditions of the Petersen-Middleton theorem are met. We see that the spectral repetitions do not overlap and hence the original spectrum can be exactly recovered.

Aliasing

The theorem gives conditions on sampling lattices for perfect reconstruction of the sampled. If the lattices are not fine enough to satisfy the Petersen-Middleton condition, then the field cannot be reconstructed exactly from the samples in general. In this case we say that the samples may be aliased. Again, consider the example in which Ω is a circular disc. If the Petersen-Middleton conditions do not hold, the support of the sampled spectrum will be as shown in Figure 4. In this case the spectral repetitions overlap leading to aliasing in the reconstruction.

A simple illustration of aliasing can be obtained by studying low-resolution images. A gray-scale image can be interpreted as a function in two-dimensional space. An example of aliasing is shown in the images of brick patterns in Figure 5. The image shows the effects of aliasing when the sampling theorem's condition is not satisfied. If the lattice of pixels is not fine enough for the scene, aliasing occurs as evidenced by the appearance of the Moiré pattern in the image obtained. The image in Figure 6 is obtained when a smoothened version of the scene is sampled with the same lattice. In this case the conditions of the theorem are satisfied and no aliasing occurs.

Optimal sampling lattices

One of the objects of interest in designing a sampling scheme for wavenumber-limited fields is to identify the configuration of points that leads to the minimum sampling density, i.e., the density of sampling points per unit spatial volume in ℜ n . Typically the cost for taking and storing the measurements is proportional to the sampling density employed. Often in practice, the natural approach to sample two-dimensional fields is to sample it at points on a rectangular lattice. However, this is not always the ideal choice in terms of the sampling density. The theorem of Petersen and Middleton can be used to identify the optimal lattice for sampling fields that are wavenumber-limited to a given set Ω ⊂ ℜ d . For example, it can be shown that the lattice in ℜ 2 with minimum spatial density of points that admits perfect reconstructions of fields wavenumber-limited to a circular disc in ℜ 2 is the hexagonal lattice. As a consequence, hexagonal lattices are preferred for sampling isotropic fields in ℜ 2 .

Optimal sampling lattices have been studied in higher dimensions. Generally, optimal sphere packing lattices are ideal for sampling smooth stochastic processes while optimal sphere covering lattices are ideal for sampling rough stochastic processes.

Since optimal lattices, in general, are non-separable, designing interpolation and reconstruction filters requires non-tensor-product (i.e., non-separable) filter design mechanisms. Box splines provide a flexible framework for designing such non-separable reconstruction FIR filters that can be geometrically tailored for each lattice. Hex-splines are the generalization of B-splines for 2-D hexagonal lattices. Similarly, in 3-D and higher dimensions, Voronoi splines provide a generalization of B-splines that can be used to design non-separable FIR filters which are geometrically tailored for any lattice, including optimal lattices.

Explicit construction of ideal low-pass filters (i.e., sinc functions) generalized to optimal lattices is possible by studying the geometric properties of Brillouin zones (i.e., Ω in above) of these lattices (which are zonotopes). This approach provides a closed-form explicit representation of χ ˇ Ω ( ⋅ ) for general lattices, including optimal sampling lattices. This construction provides a generalization of the Lanczos filter in 1-D to the multidimensional setting for optimal lattices.

Applications

The Petersen–Middleton theorem is useful in designing efficient sensor placement strategies in applications involving measurement of spatial phenomena such as seismic surveys, environment monitoring and spatial audio-field measurements.