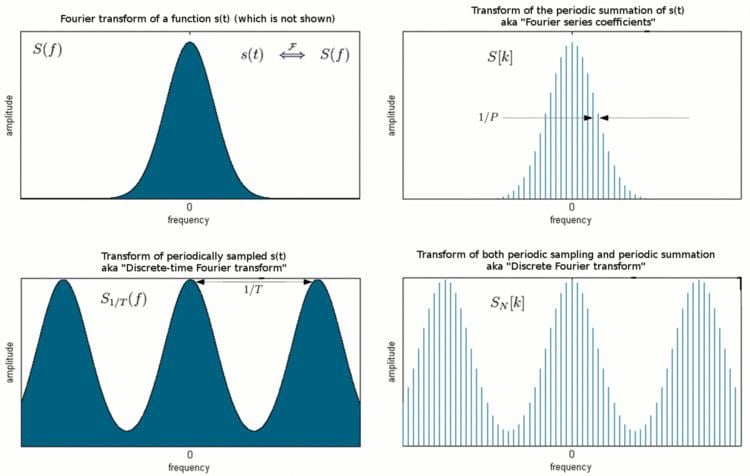
In signal processing, any periodic function
,
s
P
(
t
)
with period P, can be represented by a summation of an infinite number of instances of an aperiodic function
,
s
(
t
)
,
that are offset by integer multiples of P. This representation is called periodic summation:
s
P
(
t
)
=
∑
n
=
−
∞
∞
s
(
t
+
n
P
)
=
∑
n
=
−
∞
∞
s
(
t
−
n
P
)
.
When
s
P
(
t
)
is alternatively represented as a complex Fourier series, the Fourier coefficients are proportional to the values (or "samples") of the continuous Fourier transform
,
S
(
f
)
=
d
e
f
F
{
s
(
t
)
}
,
at intervals of 1/P. That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of
s
(
t
)
at constant intervals (T) is equivalent to a periodic summation of
S
(
f
)
,
which is known as a discrete-time Fourier transform.
The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.
Quotient space as domain
If a periodic function is represented using the quotient space domain
R
/
(
P
Z
)
then one can write
φ
P
:
R
/
(
P
Z
)
→
R
φ
P
(
x
)
=
∑
τ
∈
x
s
(
τ
)
instead. The arguments of
φ
P
are equivalence classes of real numbers that share the same fractional part when divided by
P
.