Samiksha Jaiswal (Editor)

Box spline

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Box spline httpsuploadwikimediaorgwikipediacommonsaa

In the mathematical fields of numerical analysis and approximation theory, box splines are piecewise polynomial functions of several variables. Box splines are considered as a multivariate generalization of basis splines (B-splines) and are generally used for multivariate approximation/interpolation. Geometrically, a box spline is the shadow (X-ray) of a hypercube projected down to a lower-dimensional space. Box splines and simplex splines are well studied special cases of polyhedral splines which are defined as shadows of general polytopes.

Contents

Definition

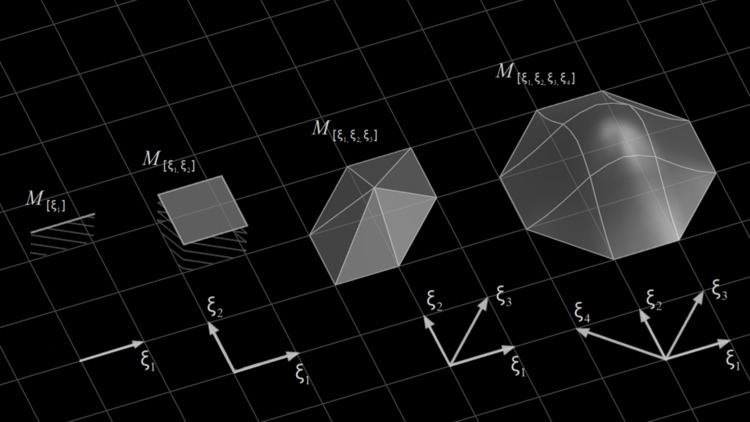
A box spline is a multivariate function ( R d → R ) defined for a set of vectors, ξ ∈ R d , usually gathered in a matrix Ξ := [ ξ 1 … ξ N ] .

When the number of vectors is the same as the dimension of the domain (i.e., N = d ) then the box spline is simply the (normalized) indicator function of the parallelepiped formed by the vectors in Ξ :

M Ξ ( x ) := 1 ∣ det Ξ ∣ χ Ξ ( x ) = { 1 ∣ det Ξ ∣ x = ∑ n = 1 d t n ξ n  for some  0 ≤ t n < 1 0 otherwise .

Adding a new direction, ξ , to Ξ , or generally when N > d , the box spline is defined recursively:

M Ξ ∪ ξ ( x ) = ∫ 0 1 M Ξ ( x − t ξ ) d t .

The box spline M Ξ can be interpreted as the shadow of the indicator function of the unit hypercube in R N when projected down into R d . In this view, the vectors ξ ∈ Ξ are the geometric projection of the standard basis in R N (i.e., the edges of the hypercube) to R d .

Considering tempered distributions a box spline associated with a single direction vector is a Dirac-like generalized function supported on t ξ for 0 ≤ t < 1 . Then the general box spline is defined as the convolution of distributions associated the single-vector box splines:

M Ξ = M ξ 1 ∗ M ξ 2 ⋯ ∗ M ξ N .

Properties

  • Let κ be the minimum number of directions whose removal from Ξ makes the remaining directions not span R d . Then the box spline has κ − 2 degrees of continuity: M Ξ ∈ C κ − 2 ( R d ) .
  • When N ≥ d (and vectors in Ξ span R d ) the box spline is a compactly supported function whose support is a zonotope in R d formed by the Minkowski sum of the direction vectors ξ ∈ Ξ .
  • Since zonotopes are centrally symmetric, the support of the box spline is symmetric with respect to its center: c Ξ := 1 2 ∑ n = 1 N ξ n .
  • Fourier transform of the box spline, in d dimensions, is given by

    • Applications

    For applications, linear combinations of shifts of one or more box splines on a lattice are used. Such splines are efficient, more so than linear combinations of simplex splines, because they are refinable and, by definition, shift invariant. They therefore form the starting point for many subdivision surface constructions.

    Box splines have been useful in characterization of hyperplane arrangements. Also, box splines can be used to compute the volume of polytopes.

    In the context of multidimensional signal processing, box splines can provide multivariate interpolation kernels (reconstruction filters) tailored to non-Cartesian sampling lattices, and crystallographic lattices (root lattices) that include many information-theoretically optimal sampling lattices. Generally, optimal sphere packing and sphere covering lattices are useful for sampling multivariate functions in 2-D, 3-D and higher dimensions. In the 2-D setting the three-direction box spline is used for interpolation of hexagonally sampled images. In the 3-D setting, four-direction and six-direction box splines are used for interpolation of data sampled on the (optimal) body centered cubic and face centered cubic lattices respectively. The seven-direction box spline has been used for modelling surfaces and can be used for interpolation of data on the Cartesian lattice as well as the body centered cubic lattice. Generalization of the four- and six-direction box splines to higher dimensions can be used to build splines on root lattices. Box splines are key ingredients of hex-splines and Voronoi splines that, however, are not refinable.

    Box splines have found applications in high-dimensional filtering, specifically for fast bilateral filtering and non-local means algorithms. Moreover, box splines are used for designing efficient space-variant (i.e., non-convolutional) filters.

    Box splines are useful basis functions for image representation in the context of tomographic reconstruction problems as the spline spaces generated by box splines spaces are closed under X-ray and Radon transforms. In this application while the signal is represented in shift-invariant spaces, the projections are obtained, in closed-form, by non-uniform translates of box splines.

    In the context of image processing, box spline frames have been shown to be effective in edge detection.

    References

    Box spline Wikipedia
    (Text) CC BY-SA


    Similar Topics