Long short term memory - Alchetron, The Free Social Encyclopedia

Long short-term memory (LSTM) is a recurrent neural network (RNN) architecture (an artificial neural network) proposed in 1997 by Sepp Hochreiter and Jürgen Schmidhuber. Like most RNNs, an LSTM network is universal in the sense that given enough network units it can compute anything a conventional computer can compute, provided it has the proper weight matrix, which may be viewed as its program. Unlike traditional RNNs, an LSTM network is well-suited to learn from experience to classify, process and predict time series when there are time lags of unknown size and bound between important events. Relative insensitivity to gap length gives an advantage to LSTM over alternative RNNs and hidden Markov models and other sequence learning methods in numerous applications. Among other successes, LSTM achieved the best known results in natural language text compression, unsegmented connected handwriting recognition, and in 2009 won the ICDAR handwriting competition. LSTM networks have also been used for automatic speech recognition, and were a major component of a network that in 2013 achieved a record 17.7% phoneme error rate on the classic TIMIT natural speech dataset. As of 2016, major technology companies including Google, Apple, Microsoft, and Baidu are using LSTM networks as fundamental components in new products.

Architecture

An LSTM network is an artificial neural network that contains LSTM units instead of, or in addition to, other network units. An LSTM unit is a recurrent network unit that excels at remembering values for either long or short durations of time. The key to this ability is that it uses no activation function within its recurrent components. Thus, the stored value is not iteratively squashed over time, and the gradient or blame term does not tend to vanish when Backpropagation through time is applied to train it.

LSTM units are often implemented in "blocks" containing several LSTM units. This design is typical with "deep" multi-layered neural networks, and facilitates implementations with parallel hardware. In the equations below, each variable in lowercase italics represents a vector with a size equal to the number of LSTM units in the block.

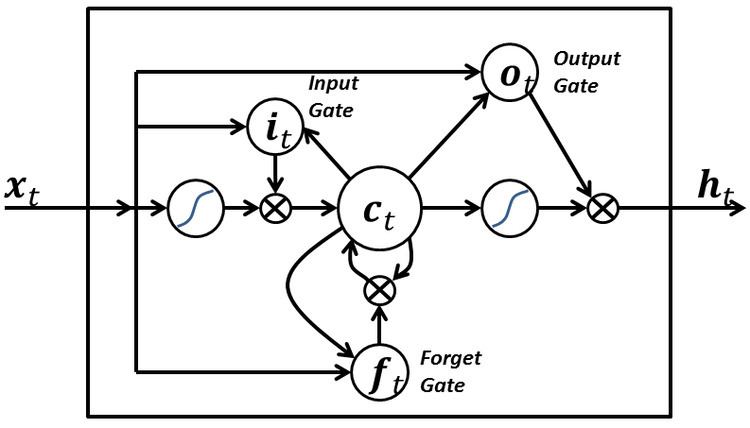
LSTM blocks contain three or four "gates" that they use to control the flow of information into or out of their memory. These gates are implemented using the logistic function to compute a value between 0 and 1. Multiplication is applied with this value to partially allow or deny information to flow into or out of the memory. For example, an "input gate" controls the extent to which a new value flows into the memory. A "forget gate" controls the extent to which a value remains in memory. And, an "output gate" controls the extent to which the value in memory is used to compute the output activation of the block. (In some implementations, the input gate and forget gate are combined into a single gate. The intuition for combining them is that the time to forget is when a new value worth remembering becomes available.)

The only weights in an LSTM block ( W and U ) are used to direct the operation of the gates. These weights occur between the values that feed into the block (including the input vector x t , and the output from the previous time step h t − 1 ) and each of the gates. Thus, the LSTM block determines how to maintain its memory as a function of those values, and training its weights causes the LSTM block to learn the function that minimizes loss. LSTM blocks are usually trained with Backpropagation through time.

Traditional LSTM

Traditional LSTM with forget gates. c 0 = 0 and h 0 = 0 . ∘ denotes the Hadamard product.

f t = σ g ( W f x t + U f h t − 1 + b f ) i t = σ g ( W i x t + U i h t − 1 + b i ) o t = σ g ( W o x t + U o h t − 1 + b o ) c t = f t ∘ c t − 1 + i t ∘ σ c ( W c x t + U c h t − 1 + b c ) h t = o t ∘ σ h ( c t )

Variables

x t : input vector

h t : output vector

c t : cell state vector

W , U and b : parameter matrices and vector

f t , i t and o t : gate vectors

f t : Forget gate vector. Weight of remembering old information.

i t : Input gate vector. Weight of acquiring new information.

o t : Output gate vector. Output candidate.

Activation functions

σ g : The original is a sigmoid function.

σ c : The original is a hyperbolic tangent.

σ h : The original is a hyperbolic tangent, but the peephole LSTM paper suggests σ h ( x ) = x .

Peephole LSTM

Peephole LSTM with forget gates. h t − 1 is not used, c t − 1 is used instead in most places.

f t = σ g ( W f x t + U f c t − 1 + b f ) i t = σ g ( W i x t + U i c t − 1 + b i ) o t = σ g ( W o x t + U o c t − 1 + b o ) c t = f t ∘ c t − 1 + i t ∘ σ c ( W c x t + b c ) h t = o t ∘ σ h ( c t )

Convolutional LSTM

Convolutional LSTM. ∗ denotes the convolution operator.

f t = σ g ( W f ∗ x t + U f ∗ h t − 1 + V f ∘ c t − 1 + b f ) i t = σ g ( W i ∗ x t + U i ∗ h t − 1 + V i ∘ c t − 1 + b i ) o t = σ g ( W o ∗ x t + U o ∗ h t − 1 + V o ∘ c t − 1 + b o ) c t = f t ∘ c t − 1 + i t ∘ σ c ( W c ∗ x t + U c ∗ h t − 1 + b c ) h t = o t ∘ σ h ( c t )

Training

To minimize LSTM's total error on a set of training sequences, iterative gradient descent such as backpropagation through time can be used to change each weight in proportion to its derivative with respect to the error. A major problem with gradient descent for standard RNNs is that error gradients vanish exponentially quickly with the size of the time lag between important events, as first realized in 1991. With LSTM blocks, however, when error values are back-propagated from the output, the error becomes trapped in the memory portion of the block. This is referred to as an "error carousel", which continuously feeds error back to each of the gates until they become trained to cut off the value. Thus, regular backpropagation is effective at training an LSTM block to remember values for very long durations.

LSTM can also be trained by a combination of artificial evolution for weights to the hidden units, and pseudo-inverse or support vector machines for weights to the output units. In reinforcement learning applications LSTM can be trained by policy gradient methods, evolution strategies or genetic algorithms.

Applications

Applications of LSTM include:

Robot control

Time series prediction

Speech recognition

Rhythm learning

Music composition

Grammar learning

Handwriting recognition

Human action recognition

Protein Homology Detection

References

Long short-term memory Wikipedia

(Text) CC BY-SA

Contents