Hadamard product (matrices)

Definition

For two matrices, A , B , of the same dimension, m × n , the Hadamard product, A ∘ B , is a matrix, of the same dimension as the operands, with elements given by

( A ∘ B ) i , j = ( A ) i , j ( B ) i , j .

For matrices of different dimensions ( m × n and p × q , where m ≠ p or n ≠ q or both) the Hadamard product is undefined.

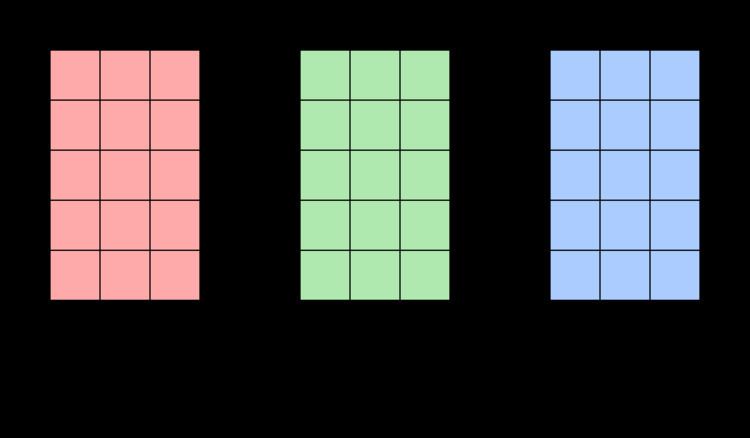
Example

For example, the Hadamard product for a 3×3 matrix A with a 3×3 matrix B is:

( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) ∘ ( b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 ) = ( a 11 b 11 a 12 b 12 a 13 b 13 a 21 b 21 a 22 b 22 a 23 b 23 a 31 b 31 a 32 b 32 a 33 b 33 )

Properties

The Hadamard product is commutative, associative and distributive over addition. That is,

A ∘ B = B ∘ A , A ∘ ( B ∘ C ) = ( A ∘ B ) ∘ C , A ∘ ( B + C ) = A ∘ B + A ∘ C .

The identity matrix under Hadamard multiplication of two m-by-n matrices is an m-by-n matrix where all elements are equal to 1. This is different from the identity matrix under regular matrix multiplication, where only the elements of the main diagonal are equal to 1. Furthermore, a matrix has an inverse under Hadamard multiplication if and only if none of the elements are equal to zero.

For vectors x and y , and corresponding diagonal matrices D x and D y with these vectors as their leading diagonals, the following identity holds:

x ∗ ( A ∘ B ) y = t r ( D x ∗ A D y B T ) , where x ∗ denotes the conjugate transpose of x . In particular, using vectors of ones, this shows that the sum of all elements in the Hadamard product is the trace of A B T . A related result for square A and B , is that the row-sums of their Hadamard product are the diagonal elements of A B T : ∑ i ( A ∘ B ) i , j = ( B T A ) j , j . ∑ j ( A ∘ B ) i , j = ( A B T ) i , i .

The Hadamard product is a principal submatrix of the Kronecker product.

The Hadamard product satisfies the rank inequality

rank ⁡ ( A ∘ B ) ≤ rank ⁡ ( A ) rank ⁡ ( B )

If A and B are positive-definite matrices, then the following inequality involving the Hadamard product is valid:

∏ i = k n λ i ( A ∘ B ) ≥ ∏ i = k n λ i ( A B ) , k = 1 , … , n , where λ i ( A ) is the ith largest eigenvalue of A .

Schur product theorem

The Hadamard product of two positive-semidefinite matrices is positive-semidefinite. This is known as the Schur product theorem, after German mathematician Issai Schur. For positive-semidefinite matrices A and B, it is also known that

det ( A ∘ B ) ≥ det ( A ) det ( B ) .

In programming languages

Hadamard multiplication is built into certain programming languages under various names. In MATLAB, GNU Octave and GAUSS, it is known as array multiplication, with the symbol .*. In Fortran, R, J and Wolfram Language (Mathematica), it is done through simple multiplication operator *, whereas the matrix product is done through the function matmul, %*%, +/ .* and the . operators, respectively. In Python with the numpy numerical library or the sympy symbolic library, multiplication of array objects as a1*a2 produces the Hadamard product, but with otherwise matrix objects m1*m2 will produce a matrix product. The Eigen C++ library provides a cwiseProduct member function for the Matrix class (a.cwiseProduct(b)), while the Armadillo library use the operator % to make compact expressions (a % b; a * b is a matrix product).

Applications

The Hadamard product appears in lossy compression algorithms such as JPEG. The decoding step involves an entry-for-entry product, i.e., Hadamard product.

Analogous operations

Other Hadamard operations are also seen in the mathematical literature, namely the Hadamard root and Hadamard power (which are in effect the same thing because of fractional indices), defined for a matrix such that: For

B = A ∘ 2 B i j = A i j 2

and for

B = A ∘ 1 2 B i j = A i j 1 2

The Hadamard inverse reads:

B = A ∘ − 1 B i j = A i j − 1

A Hadamard division is defined as:

C = A ⊘ B C i j = A i j / B i j