Average Worst case | ||
 | ||
O ( n ) {displaystyle {mathcal {O}}(n)} O ( n ) {displaystyle {mathcal {O}}(n)} O ( n ) {displaystyle {mathcal {O}}(n)} O ( n ) {displaystyle {mathcal {O}}(n)} | ||
In computer science, the longest common prefix array (LCP array) is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.
Contents
- History
- Definition
- Example
- Difference between suffix array and LCP array
- LCP array usage in finding the number of occurrences of a pattern
- Efficient construction algorithms
- Applications
- Suffix tree construction
- LCP queries for arbitrary suffixes
- References
For example, if A := [aab, ab, abaab, b, baab] is a suffix array, the longest common prefix between A[1] = aab and A[2] = ab is a which has length 1, so H[2] = 1 in the LCP array H. Likewise, the LCP of A[2] = ab and A[3] = abaab is ab, so H[3] = 2.
Augmenting the suffix array with the LCP array allows one to efficiently simulate top-down and bottom-up traversals of the suffix tree, speeds up pattern matching on the suffix array and is a prerequisite for compressed suffix trees.
History
The LCP array was introduced in 1993, by Udi Manber and Gene Myers alongside the suffix array in order to improve the running time of their string search algorithm. Gene Myers later became the vice president of Informatics Research at Celera Genomics, and Udi Manber the vice president of engineering at Google.
Definition
Let
Then the LCP array
Example
Consider the string
and its corresponding sorted suffix array
Complete suffix array with sorted suffixes itself:
Then the LCP array
So, for example,
Difference between suffix array and LCP array
Suffix array: Represents the lexicographic rank of each suffix of an array.
LCP array: Contains the maximum length prefix match between two consecutive suffixes, after they are sorted lexicographically.
LCP array usage in finding the number of occurrences of a pattern
In order to find the number of occurrences of a given string P (length m) in a text T (length N),
The issue with using standard binary search (without the LCP information) is that in each of the O(log N) comparisons you need to make, you compare P to the current entry of the suffix array, which means a full string comparison of up to m characters. So the complexity is O(m*log N).
The LCP-LR array helps improve this to O(m+log N), in the following way:
At any point during the binary search algorithm, you consider, as usual, a range (L,...,R) of the suffix array and its central point M, and decide whether you continue your search in the left sub-range (L,...,M) or in the right sub-range (M,...,R). In order to make the decision, you compare P to the string at M. If P is identical to M, you are done, but if not, you will have compared the first k characters of P and then decided whether P is lexicographically smaller or larger than M. Let's assume the outcome is that P is larger than M. So, in the next step, you consider (M,...,R) and a new central point M' in the middle:
M ...... M' ...... R | we know: lcp(P,M)==kThe trick now is that LCP-LR is precomputed such that an O(1)-lookup tells you the longest common prefix of M and M', lcp(M,M').
You know already (from the previous step) that M itself has a prefix of k characters in common with P: lcp(P,M)=k. Now there are three possibilities:
The overall effect is that no character of P is compared to any character of the text more than once. The total number of character comparisons is bounded by m, so the total complexity is indeed O(m+log N).
Obviously, the key remaining question is how did we precompute LCP-LR so it is able to tell us in O(1) time the lcp between any two entries of the suffix array? As you said, the standard LCP array tells you the lcp of consecutive entries only, i.e. lcp(x-1,x) for any x. But M and M' in the description above are not necessarily consecutive entries, so how is that done?
The key to this is to realize that only certain ranges (L,...,R) will ever occur during the binary search: It always starts with (0,...,N) and divides that at the center, and then continues either left or right and divide that half again and so forth. If you think of it: Every entry of the suffix array occurs as central point of exactly one possible range during binary search. So there are exactly N distinct ranges (L...M...R) that can possibly play a role during binary search, and it suffices to precompute lcp(L,M) and lcp(M,R) for those N possible ranges. So that is 2*N distinct precomputed values, hence LCP-LR is O(N) in size.
Moreover, there is a straightforward recursive algorithm to compute the 2*N values of LCP-LR in O(N) time from the standard LCP array – I'd suggest posting a separate question if you need a detailed description of that.
To sum up:
Efficient construction algorithms
LCP array construction algorithms can be divided into two different categories: algorithms that compute the LCP array as a byproduct to the suffix array and algorithms that use an already constructed suffix array in order to compute the LCP values.
Manber & Myers (1993) provide an algorithm to compute the LCP array alongside the suffix array in
Assuming that each text symbol takes one byte and each entry of the suffix or LCP array takes 4 bytes, the major drawback of their algorithm is a large space occupancy of
Gog & Ohlebusch (2011) provide two algorithms that although being theoretically slow (
As of 2012, the currently fastest linear-time LCP array construction algorithm is due to Fischer (2011), which in turn is based on one of the fastest suffix array construction algorithms by Nong, Zhang & Chan (2009).
Applications
As noted by Abouelhoda, Kurtz & Ohlebusch (2004) several string processing problems can be solved by the following kinds of tree traversals:
Kasai et al. (2001) show how to simulate a bottom-up traversal of the suffix tree using only the suffix array and LCP array. Abouelhoda, Kurtz & Ohlebusch (2004) enhance the suffix array with the LCP array and additional data structures and describe how this enhanced suffix array can be used to simulate all three kinds of suffix tree traversals. Fischer & Heun (2007) reduce the space requirements of the enhanced suffix array by preprocessing the LCP array for range minimum queries. Thus, every problem that can be solved by suffix tree algorithms can also be solved using the enhanced suffix array.
Deciding if a pattern
The LCP array is also an essential part of compressed suffix trees which provide full suffix tree functionality like suffix links and lowest common ancestor queries. Furthermore, it can be used together with the suffix array to compute the Lempel-Ziv LZ77 factorization in
The longest repeated substring problem for a string
The remainder of this section explains two applications of the LCP array in more detail: How the suffix array and the LCP array of a string can be used to construct the corresponding suffix tree and how it is possible to answer LCP queries for arbitrary suffixes using range minimum queries on the LCP array.
Suffix tree construction
Given the suffix array
Let
Start with
We need to distinguish two cases:
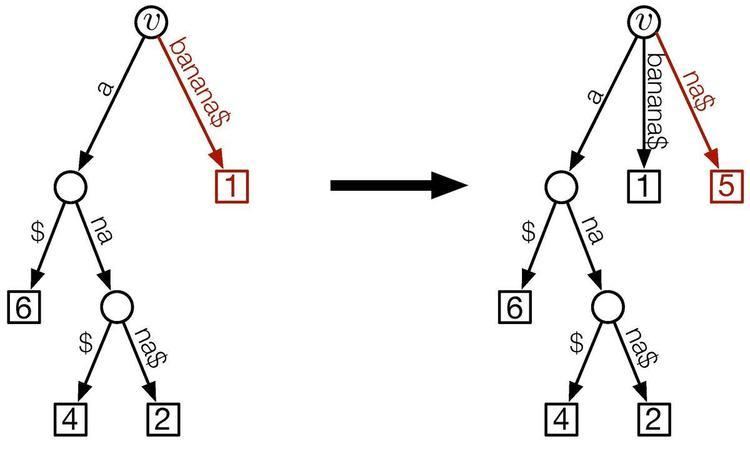
In this case, insert
This creates the partial suffix tree
Let
- Delete the edge
( v , w ) . - Add a new internal node
y and a new edge( v , y ) with labelS [ A [ i ] + d ( v ) , A [ i ] + H [ i + 1 ] − 1 ] . The new label consists of the missing characters of the longest common prefix ofA [ i ] andA [ i + 1 ] . Thus, the concatenation of the labels of the root-to-y path now displays the longest common prefix ofA [ i ] andA [ i + 1 ] . - Connect
w to the newly created internal nodey by an edge( y , w ) that is labeledS [ A [ i ] + H [ i + 1 ] , A [ i ] + d ( w ) − 1 ] . The new label consists of the remaining characters of the deleted edge( v , w ) that were not used as the label of edge( v , y ) . - Add
A [ i + 1 ] as a new leafx and connect it to the new internal nodey by an edge( y , x ) that is labeledS [ A [ i + 1 ] + H [ i + 1 ] , n ] . Thus the edge label consists of the remaining characters of suffixA [ i + 1 ] that are not already represented by the concatenation of the labels of the root-to-v path. - This creates the partial suffix tree
S T i + 1
A simple amortization argument shows that the running time of this algorithm is bounded by
The nodes that are traversed in step
LCP queries for arbitrary suffixes
The LCP array
Because of the lexicographic order of the suffix array, every common prefix of the suffixes
Thus given a string
