 | ||
In mathematics, the isoperimetric inequality is a geometric inequality involving the surface area of a set and its volume. In
Contents
- The isoperimetric problem in the plane
- Isoperimetric inequality on a plane
- Isoperimetric inequality on a sphere
- Isoperimetric inequality in R n displaystyle mathbb R n
- Isoperimetric inequalities in a metric measure space
- Isoperimetric inequalities for graphs
- Example Isoperimetric inequalities for hypercubes
- Edge isoperimetric inequality
- Vertex isoperimetric inequality
- Isoperimetric inequality for triangles
- References
where
On a plane, i.e. when
and that equality holds if and only if the curve is a circle.
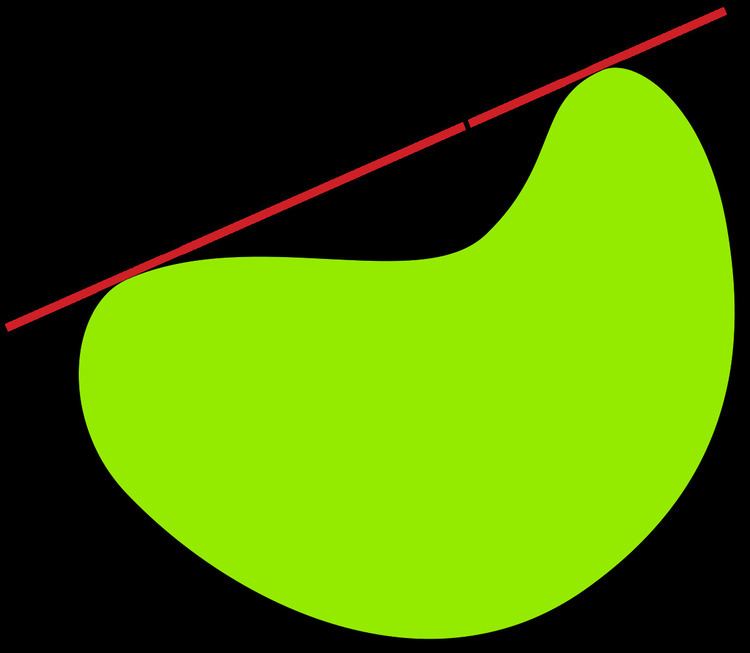
The isoperimetric problem is to determine a plane figure of the largest possible area whose boundary has a specified length. The closely related Dido's problem asks for a region of the maximal area bounded by a straight line and a curvilinear arc whose endpoints belong to that line. It is named after Dido, the legendary founder and first queen of Carthage. The solution to the isoperimetric problem is given by a circle and was known already in Ancient Greece. However, the first mathematically rigorous proof of this fact was obtained only in the 19th century. Since then, many other proofs have been found.
The isoperimetric problem has been extended in multiple ways, for example, to curves on surfaces and to regions in higher-dimensional spaces. Perhaps the most familiar physical manifestation of the 3-dimensional isoperimetric inequality is the shape of a drop of water. Namely, a drop will typically assume a symmetric round shape. Since the amount of water in a drop is fixed, surface tension forces the drop into a shape which minimizes the surface area of the drop, namely a round sphere.
The isoperimetric problem in the plane
The classical isoperimetric problem dates back to antiquity. The problem can be stated as follows: Among all closed curves in the plane of fixed perimeter, which curve (if any) maximizes the area of its enclosed region? This question can be shown to be equivalent to the following problem: Among all closed curves in the plane enclosing a fixed area, which curve (if any) minimizes the perimeter?
This problem is conceptually related to the principle of least action in physics, in that it can be restated: what is the principle of action which encloses the greatest area, with the greatest economy of effort? The 15th-century philosopher and scientist, Cardinal Nicholas of Cusa, considered rotational action, the process by which a circle is generated, to be the most direct reflection, in the realm of sensory impressions, of the process by which the universe is created. German astronomer and astrologer Johannes Kepler invoked the isoperimetric principle in discussing the morphology of the solar system, in Mysterium Cosmographicum (The Sacred Mystery of the Cosmos, 1596).
Although the circle appears to be an obvious solution to the problem, proving this fact is rather difficult. The first progress toward the solution was made by Swiss geometer Jakob Steiner in 1838, using a geometric method later named Steiner symmetrisation. Steiner showed that if a solution existed, then it must be the circle. Steiner's proof was completed later by several other mathematicians.
Steiner begins with some geometric constructions which are easily understood; for example, it can be shown that any closed curve enclosing a region that is not fully convex can be modified to enclose more area, by "flipping" the concave areas so that they become convex. It can further be shown that any closed curve which is not fully symmetrical can be "tilted" so that it encloses more area. The one shape that is perfectly convex and symmetrical is the circle, although this, in itself, does not represent a rigorous proof of the isoperimetric theorem (see external links).
Isoperimetric inequality on a plane
The solution to the isoperimetric problem is usually expressed in the form of an inequality that relates the length L of a closed curve and the area A of the planar region that it encloses. The isoperimetric inequality states that
and that the equality holds if and only if the curve is a circle. Indeed, the area of a disk of radius R is πR2 and the circumference of the circle is 2πR, so both sides of the inequality are equal to 4π2R2 in this case.
Dozens of proofs of the isoperimetric inequality have been found. In 1902, Hurwitz published a short proof using the Fourier series that applies to arbitrary rectifiable curves (not assumed to be smooth). An elegant direct proof based on comparison of a smooth simple closed curve with an appropriate circle was given by E. Schmidt in 1938. It uses only the arc length formula, expression for the area of a plane region from Green's theorem, and the Cauchy–Schwarz inequality.
For a given closed curve, the isoperimetric quotient is defined as the ratio of its area and that of the circle having the same perimeter. This is equal to
and the isoperimetric inequality says that Q ≤ 1. Equivalently, the isoperimetric ratio L2/A is at least 4π for every curve.
The isoperimetric quotient of a regular n-gon is
Let
where
Isoperimetric inequality on a sphere
Let C be a simple closed curve on a sphere of radius 1. Denote by L the length of C and by A the area enclosed by C. The spherical isoperimetric inequality states that
and that the equality holds if and only if the curve is a circle. There are, in fact, two ways to measure the spherical area enclosed by a simple closed curve, but the inequality is symmetric with the respect to taking the complement.
This inequality was discovered by Paul Lévy (1919) who also extended it to higher dimensions and general surfaces.
In the more general case of arbitrary radius R, it is known that
Isoperimetric inequality in R n {displaystyle mathbb {R} ^{n}}
The isoperimetric inequality states that a sphere has the smallest surface area per given volume. Given a set
where
The proof on the inequality follows directly from Brunn-Minkowski inequality between a set
In full generality (Federer 1969, §3.2.43), the isoperimetric inequality states that for any set
where
The n-dimensional isoperimetric inequality is equivalent (for sufficiently smooth domains) to the Sobolev inequality on
for all
Isoperimetric inequalities in a metric measure space
Most of the work on isoperimetric problem has been done in the context of smooth regions in Euclidean spaces, or more generally, in Riemannian manifolds. However, the isoperimetric problem can be formulated in much greater generality, using the notion of Minkowski content. Let
where
is the ε-extension of A.
The isoperimetric problem in X asks how small can
The function
is called the isoperimetric profile of the metric measure space
Isoperimetric inequalities for graphs
In graph theory, isoperimetric inequalities are at the heart of the study of expander graphs, which are sparse graphs that have strong connectivity properties. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes.
Isoperimetric inequalities for graphs relate the size of vertex subsets to the size of their boundary, which is usually measured by the number of edges leaving the subset (edge expansion) or by the number of neighbouring vertices (vertex expansion). For a graph
Here
Example: Isoperimetric inequalities for hypercubes
The
Edge isoperimetric inequality
The edge isoperimetric inequality of the hypercube is
Vertex isoperimetric inequality
Harper's theorem says that Hamming balls have the smallest vertex boundary among all sets of a given size. Hamming balls are sets that contain all points of Hamming weight at most
As a special case, consider set sizes
Isoperimetric inequality for triangles
The isoperimetric inequality for triangles in terms of perimeter p and area T states that
with equality for the equilateral triangle. This is implied, via the geometric-algebraic mean inequality, by a stronger inequality which has also been called the isoperimetric inequality for triangles:
