Inverse limit

Algebraic objects

We start with the definition of an inverse system (or projective system) of groups and homomorphisms. Let (I, ≤) be a directed poset (not all authors require I to be directed). Let (A_i)_i∈I be a family of groups and suppose we have a family of homomorphisms f_ij: A_j → A_i for all i ≤ j (note the order), called bonding maps, with the following properties:

1. f_ii is the identity on A_i,
2. f_ik = f_ij o f_jk for all i ≤ j ≤ k.

Then the pair ((A_i)_i∈I, (f_ij)_{i≤ j∈I}) is called an inverse system of groups and morphisms over I, and the morphisms f_ij are called the transition morphisms of the system.

We define the inverse limit of the inverse system ((A_i)_i∈I, (f_ij)_{i≤ j∈I}) as a particular subgroup of the direct product of the A_i's:

The inverse limit, A, comes equipped with natural projections π_i: A → A_i which pick out the ith component of the direct product for each i in I. The inverse limit and the natural projections satisfy a universal property described in the next section.

This same construction may be carried out if the A_i's are sets, semigroups, topological spaces, rings, modules (over a fixed ring), algebras (over a fixed ring), etc., and the homomorphisms are morphisms in the corresponding category. The inverse limit will also belong to that category.

General definition

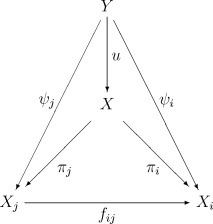
The inverse limit can be defined abstractly in an arbitrary category by means of a universal property. Let (X_i, f_ij) be an inverse system of objects and morphisms in a category C (same definition as above). The inverse limit of this system is an object X in C together with morphisms π_i: X → X_i (called projections) satisfying π_i = f_ij o π_j for all i ≤ j. The pair (X, π_i) must be universal in the sense that for any other such pair (Y, ψ_i) (i.e. ψ_i: Y → X_i with ψ_i = f_ij o ψ_j for all i ≤ j) there exists a unique morphism u: Y → X such that the diagram

commutes for all i ≤ j, for which it suffices to show that ψ_i = π_i o u for all i. The inverse limit is often denoted

with the inverse system (X_i, f_ij) being understood.

In some categories, the inverse limit does not exist. If it does, however, it is unique in a strong sense: given any other inverse limit X′ there exists a unique isomorphism X′ → X commuting with the projection maps.

We note that an inverse system in a category C admits an alternative description in terms of functors. Any partially ordered set I can be considered as a small category where the morphisms consist of arrows i → j if and only if i ≤ j. An inverse system is then just a contravariant functor I → C. And the inverse limit functor lim ← : C I o p → C is a covariant functor.

Examples

Derived functors of the inverse limit

For an abelian category C, the inverse limit functor

is left exact. If I is ordered (not simply partially ordered) and countable, and C is the category Ab of abelian groups, the Mittag-Leffler condition is a condition on the transition morphisms f_ij that ensures the exactness of lim ← . Specifically, Eilenberg constructed a functor

(pronounced "lim one") such that if (A_i, f_ij), (B_i, g_ij), and (C_i, h_ij) are three projective systems of abelian groups, and

is a short exact sequence of inverse systems, then

is an exact sequence in Ab.

Mittag-Leffler condition

If the ranges of the morphisms of an inverse system of abelian groups (A_i, f_ij) are stationary, that is, for every k there exists j ≥ k such that for all i ≥ j : f k j ( A j ) = f k i ( A i ) one says that the system satisfies the Mittag-Leffler condition. This condition implies that lim ← ⁡ 1 A i = 0.

The name "Mittag-Leffler" for this condition was given by Bourbaki in their chapter on uniform structures for a similar result about inverse limits of complete Hausdorff uniform spaces. Mittag-Leffler used a similar argument in the proof of Mittag-Leffler's theorem.

The following situations are examples where the Mittag-Leffler condition is satisfied:

An example where lim ← ⁡ 1 is non-zero is obtained by taking I to be the non-negative integers, letting A_i = pⁱZ, B_i = Z, and C_i = B_i / A_i = Z/pⁱZ. Then

where Z_p denotes the p-adic integers.

Further results

More generally, if C is an arbitrary abelian category that has enough injectives, then so does C^I, and the right derived functors of the inverse limit functor can thus be defined. The nth right derived functor is denoted

In the case where C satisfies Grothendieck's axiom (AB4*), Jan-Erik Roos generalized the functor lim¹ on Ab^I to series of functors limⁿ such that

It was thought for almost 40 years that Roos had proved (in Sur les foncteurs dérivés de lim. Applications. ) that lim¹ A_i = 0 for (A_i, f_ij) an inverse system with surjective transition morphisms and I the set of non-negative integers (such inverse systems are often called "Mittag-Leffler sequences"). However, in 2002, Amnon Neeman and Pierre Deligne constructed an example of such a system in a category satisfying (AB4) (in addition to (AB4*)) with lim¹ A_i ≠ 0. Roos has since shown (in "Derived functors of inverse limits revisited") that his result is correct if C has a set of generators (in addition to satisfying (AB3) and (AB4*)).

Barry Mitchell has shown (in "The cohomological dimension of a directed set") that if I has cardinality ℵ d (the dth infinite cardinal), then Rⁿlim is zero for all n ≥ d + 2. This applies to the I-indexed diagrams in the category of R-modules, with R a commutative ring; it is not necessarily true in an arbitrary abelian category (see Roos' "Derived functors of inverse limits revisited" for examples of abelian categories in which limⁿ, on diagrams indexed by a countable set, is nonzero for n > 1).

Related concepts and generalizations

The categorical dual of an inverse limit is a direct limit (or inductive limit). More general concepts are the limits and colimits of category theory. The terminology is somewhat confusing: inverse limits are limits, while direct limits are colimits.