Homomorphism

Definition

A homomorphism is a map between two algebraic structures of the same type (that is of the same name), that preserves the operations of the structures. This means a map f : A → B between two sets A, B equipped with the same structure such that, if ∗ is an operation of the structure (supposed here, for simplification, to be a binary operation), then

for every pair x, y of elements of A. One says often that f preserves the operation or is compatible with the operation.

Formally, a map f : A → B preserves an operation μ of arity k, defined on both A and B if

for all elements a₁, ..., a_k in A.

For example:

An algebraic structure may have more than one operation, and a homomorphism is required to preserve each operation. Thus a map that preserves only some of the operations is not a homomorphism of the structure, but only a homomorphism of the substructure obtained by considering only the preserved operations. For example, a map between monoids that preserves the monoid operation and not the identity element, is not a monoid homomorphism, but only a semigroup homomorphism.

The notation for the operations does not need to be the same in the source and the target of a homomorphism. For example, the real numbers form a group for addition, and the positive real numbers form a group for multiplication. The exponential function

satisfies

and is thus an homomorphism between these two groups. It is even an isomorphism (see below), as its inverse function, the natural logarithm, satisfies

and is also a group homomorphism.

Examples

The real numbers are a ring, having both addition and multiplication. The set of all 2 × 2 matrices is also a ring, under matrix addition and matrix multiplication. If we define a function between these rings as follows:

where r is a real number, then f is a homomorphism of rings, since f preserves both addition:

and multiplication:

For another example, the nonzero complex numbers form a group under the operation of multiplication, as do the nonzero real numbers. (Zero must be excluded from both groups since it does not have a multiplicative inverse, which is required for elements of a group.) Define a function f from the nonzero complex numbers to the nonzero real numbers by

That is, ƒ(z) is the absolute value (or modulus) of the complex number z. Then f is a homomorphism of groups, since it preserves multiplication:

Note that ƒ cannot be extended to a homomorphism of rings (from the complex numbers to the real numbers), since it does not preserve addition:

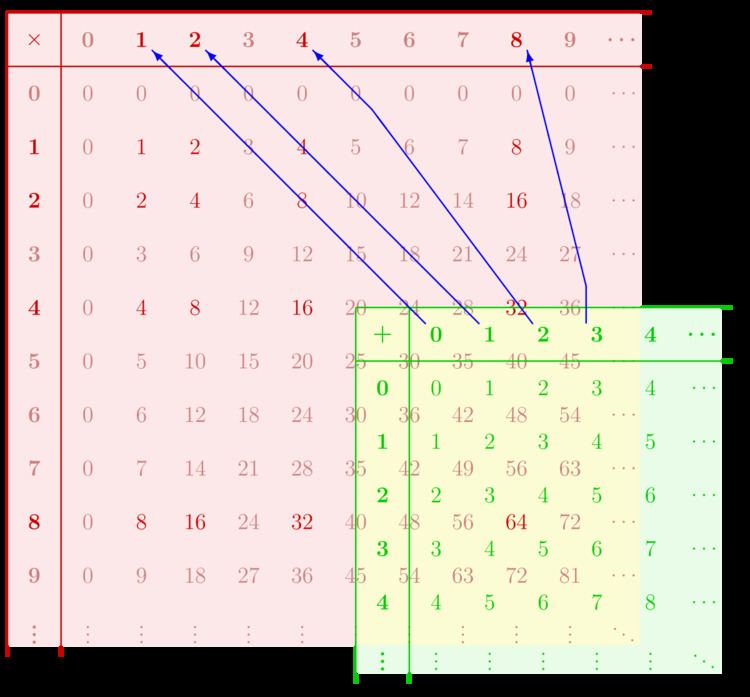
As another example, the picture shows a monoid homomorphism f from the monoid (N, +, 0) to the monoid (N, ×, 1). Due to the different names of corresponding operations, the structure preservation properties satisfied by f amount to f(x + y) = f(x) × f(y) and f(0) = 1.

Special homomorphisms

Several kinds of homomorphisms have a specific name, which is also defined for general morphisms.

Isomorphism

An isomorphism between algebraic structures of the same type is commonly defined as a bijective homomorphism.

In the more general context of category theory, an isomorphism is defined as a morphism, which has an inverse that is also a morphism. In the specific case of algebraic structures, the two definitions are equivalent, although they may differ for non-algebraic structures, which have an underlying set.

More precisely, if

is a (homo)morphism, it has an inverse if there exists an homorphism

such that

If A and B have underlying sets, and f : A → B has an inverse g, then f is bijective. In fact, f is injective, as f(x) = f(y) implies x = g(f(x)) = g(f(y)) = y, and f is surjective, as, for any x in B, one has x = f(g(x)), and x is the image of an element of A.

Conversely, if f : A → B is a bijective homomorphism between algebraic structures, let g : B → A be the map such that g(y) is the unique element x of A such that f(x) = y. One has f ∘ g = Id B ⁡  and  g ∘ f = Id A , and it remains only to shows that g is an homomorphism. If ∗ is a binary operation of the structure, for every pair x, y of elements of B, one has

and g is thus compatible with ∗ . As the proof is similar for any arity, this shows that g is an homomorphism.

This proof does not work for non-algebraic structures. For examples, for topological spaces, a morphism is a continuous map, and the inverse of a bijective continuous map needs not to be continuous. An isomorphism of topological spaces, called homeomorphism or bicontinuous map, is thus a bijective continuous map, whose inverse is also continuous.

Endomorphism

An endomorphism is an homomorphism whose domain equals the codomain, or, more generally, a morphism whose source is equal to the target.

The endomorphisms of an algebraic structure, or of an object of a category form a monoid under composition.

The endomorphisms of a vector space or of a module form a ring. In the case of a vector space or a free module of finite dimension, the choice of a basis induces a ring isomorphism between the ring of endomorphisms and the ring of square matrices of the same dimension.

Automorphism

An automorphism is an endomorphism, which also an isomorphism.

The automorphisms of an algebraic structure or of an object of a category form a group under composition, which is called the automorphism group of the structure.

Many groups that have received a name are automorphism groups of some algebraic structure. For example, the general linear group GL n ⁡ ( k ) is the automorphism group of a vector space of dimension n over a field k.

The automorphism groups of fields were introduced by Évariste Galois for studying the roots of polynomials, and are the basis of Galois theory.

Monomorphism

For algebraic structures, monomorphisms are commonly defined as injective homomorphisms.

In the more general context of category theory, a monomorphism is defined as an homomorphism that is left cancelable. This means that a (homo)morphism f : A → B is a monomorphism if, for any pair g, h of morphisms from any other object C to A, then f ∘ g = f ∘ h implies g = h.

These two definitions of monomorphism are equivalent for all common algebraic structures. More precisely, they are equivalent for fields, for which every homomorphism is a monomorphism, and for varieties of universal algebra, that is algebraic structures for which operations and axioms (identities) are defined without any restriction (fields are not a variety, as the multiplicative inverse is defined either as a unary operation or as a property of the multiplication, which are, in both cases, defined only for nonzero elements).

In particular, the two definitions of a monomorphism are equivalent for sets, magmas, semigroups, monoids, groups, rings, fields, vector spaces and modules.

A split monomorphism is an homomorphism that has a right inverse. That is, an homomorphisms f : A → B is a split homomorphism if there exists an homomorphism g : B → A such that g ∘ f = Id A . A split monomorphism is always a monomorphism, for both meanings of monomorphism. For sets and vector spaces, every monomorphism is a split homomorphism, but this property is wrong for most common algebraic structures.

Epimorphism

In algebra, epimorphisms are often defined as surjective homomorphisms. On the other hand, in category theory, epimorphisms are defined as right cancelable. This means that a (homo)morphism f : A → B is an epimorphism if, for any pair g, h of morphisms from B to any other object C, the equality g ∘ f = h ∘ f implies g = h.

A surjective homomorphism is always right cancelable, but the converse is not always true for algebraic structures. However, the two definitions of epimorphism are equivalent for sets, vector spaces, abelian groups and modules. The importance of these structures in all mathematics, and specially in linear algebra and homological algebra, may explain the coexistence of two non-equivalent definitions.

The most basic example of an epimorphism (category theory meaning), which is not surjective, is the ring inclusion of Z in Q. This is also an example of a ring homomorphism which is both a monomorphism and an epimorphism, but not an isomorphism.

A wide generalization of this example is the localization of a ring by a multiplicative set. Every localization is a ring epimorphism, which is not, in general, surjective. As localizations are fundamental in commutative algebra and algebraic geometry, this may explain why in these areas, the definition of epimorphisms as right cancelable homomorphisms is generally preferred.

A split epimorphism is an homomorphism that has a left inverse. That is, an homomorphisms f : A → B is a split epimorphism if there exists an homomorphism g : B → A such that f ∘ g = Id B . A split epimorphism is always an epimorphism, for both meanings of epimorphism. For sets and vector spaces, every epimorphism is a split epimorphism, but this property is wrong for most common algebraic structures.

In summary, one has

the last implication is an equivalence for sets, vector spaces, modules and abelian groups; the first implication is an equivalence for sets and vector spaces.

Kernel

Any homomorphism f : X → Y defines an equivalence relation ~ on X by a ~ b if and only if f(a) = f(b). The relation ~ is called the kernel of f. It is a congruence relation on X. The quotient set X / ~ can then be given a structure of the same type, in a natural way, by defining the operations as [x] ∗ [y] = [x ∗ y]. In that case the image of X in Y under the homomorphism f is necessarily isomorphic to X / ~; this fact is one of the isomorphism theorems.

When the algebraic structure is a group for some operation, the equivalence class K of the identity element of this operation suffices to characterize the equivalence relation. In ths case, the quotient by the equivalence relation is denoted by X/K (usually read as "X mod K"). Also in this case, it is K, rather than ~, that is called the kernel of f. The kernels of homomorphisms of a given type of algebraic structure are naturally equipped with some structure. This structure type of the kernels is the same as the considered structure, in the case of abelian groups, vector spaces and modules, but is different and has received a specific name in other cases, such as normal subgroup for kernels of group homomorphisms and ideals for kernels of ring homomorphisms (in the case of non-commutative rings, the kernels are the two-sided ideals).

Relational structures

In model theory, the notion of an algebraic structure is generalized to structures involving both operations and relations. Let L be a signature consisting of function and relation symbols, and A, B be two L-structures. Then a homomorphism from A to B is a mapping h from the domain of A to the domain of B such that

In the special case with just one binary relation, we obtain the notion of a graph homomorphism. For a detailed discussion of relational homomorphisms and isomorphisms see.

Formal language theory

Homomorphisms are also used in the study of formal languages (although within this context, often they are briefly referred to as morphisms). Given alphabets Σ₁ and Σ₂, a function h : Σ₁^∗ → Σ₂^∗ such that h(uv) = h(u) h(v) for all u and v in Σ₁^∗ is called a homomorphism (or simply morphism) on Σ₁^∗. Let e denote the empty word. If h is a homomorphism on Σ₁^∗ and h(x) ≠ e for all x ≠ e in Σ₁^∗, then h is called an e-free homomorphism.

This type of homomorphism can be thought of as (and is equivalent to) a monoid homomorphism where Σ^∗ the set of all words over a finite alphabet Σ is a monoid (in fact it is the free monoid on Σ) with operation concatenation and the empty word as the identity.