Interatomic potential

Functional form

Interatomic potentials can be written as a series expansion of functional terms that depend on the position of one, two, three, etc. atoms at a time. Then the total energy of the system V can be written as

Here V 1 is the one-body term, V 2 the two-body term, V 3 the three body term, N the number of atoms in the system, r → i the position of atom i, etc. i, j and k are indices that loop over atom positions.

Note that in case the pair potential is given per atom pair, in the two-body term the potential should be multiplied by 1/2 as otherwise each bond is counted twice, and similarly the three-body term by 1/6. Alternatively, the summation of the pair term can be restricted to cases i < j and similarly for the three-body term i < j < k , if the potential form is such that it is symmetric with respect to exchange of the j and k indices (this may not be the case for potentials for multielemental systems).

The one-body term is only meaningful if the atoms are in an external field (e.g. an electric field). In the absence of external fields, the potential V should not depend on the absolute position of atoms, but only on the relative positions. This means that the functional form can be rewritten as a function of interatomic distances r i j = | r → i − r → j | and angles between the bonds (vectors to neighbours) θ i j k . Then, in the absence of external forces, the general form becomes

In the three-body term V 3 the interatomic distance r j k is not needed since the three terms r i j , r i k , θ i j k are sufficient to give the relative positions of three atoms i,j,k in three-dimensional space. Any terms of order higher than 2 are also called many-body potentials. In some interatomic potentials the manybody interactions are embedded into the terms of a pair potential (see discussion on EAM-like and bond order potentials below).

In principle the sums in the expressions run over all N atoms. However, if the range of the interatomic potential is finite, i.e. the potentials V ( r ) ≡ 0 above some cutoff distance r c u t , the summing can be restricted to atoms within the cutoff distance of each other. By also using a cellular method for finding the neighbours, the MD algorithm can be an O(N) algorithm. Potentials with an infinite range can be summed up efficiently by Ewald summation and its further developments.

Force calculation

The forces acting between atoms can be obtained by differentiation of the total energy with respect to atom positions. That is, to get the force on atom i one should take the three-dimensional derivative (gradient) with respect to the position of atom i:

For two-body potentials this gradient reduces, thanks to the symmetry with respect to ij in the potential form, to straightforward differentiation with respect to the interatomic distances r i j . However, for many-body potentials (three-body, four-body, etc.) the differentiation becomes considerably more complex since the potential may not be any longer symmetric with respect to ij exchange. In other words, also the energy of atoms k that are not direct neighbours of i can depend on the position r → i because of angular and other many-body terms, and hence contribute to the gradient ∇ r → i .

Classes of interatomic potentials

Interatomic potentials come in many different varieties, with different physical motivations. Even for single well-known elements such as silicon, a wide variety of potentials quite different in functional form and motivation have been developed. The true interatomic interactions are quantum mechanical in nature, and there is no known way in which the true interactions described by the Schrödinger equation or Dirac equation for all electrons and nuclei could be cast into an analytical functional form. Hence all analytical interatomic potentials are by necessity approximations.

Pair potentials

The arguably simplest widely used interatomic interaction model is the Lennard-Jones potential

where ε is the depth of the potential well and σ is the distance at which the potential crosses zero. The term proportional to 1 / r 6 in the potential can be motivated from a classical or quantum mechanical description of the interaction between induced electric dipoles. This potential seems to be quite accurate for noble gases, and is widely used for systems where dipole interactions are significant, including in chemistry force fields to describe intermermolecular interactions.

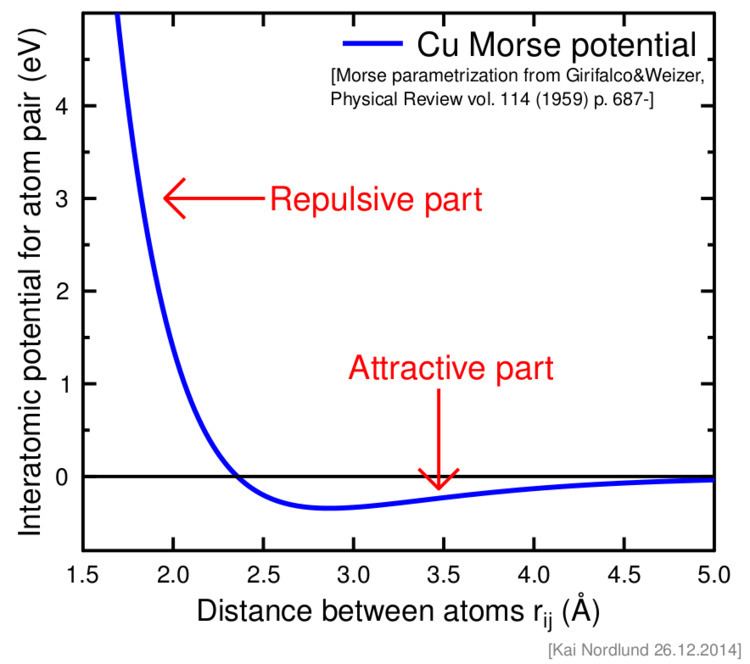
Another simple and widely used pair potential is the Morse potential, which consists simply of a sum of two exponentials.

Here D e is the equilibrium bond energy and r e the bond distance. The Morse potential has been applied to studies of molecular vibrations and solids , and although rarely used anymore, inspired the functional form of more modern potentials such as the bond-order potentials.

Ionic materials are often described by a sum of a short-range repulsive term, such as the Buckingham pair potential, and a long-range Coulomb potential giving the ionic interactions between the ions forming the material. The short-range term for ionic materials can also be of many-body character .

Pair potentials have some inherent limitations, like the inability to describe all 3 elastic constants of cubic metals. Hence modern molecular dynamics simulations are to a large extent carried out with different kinds of many-body potentials.

Many-body potentials

The Stilinger-Weber potential is a potential that has a two-body and three-body terms of the standard form

where the three-body term describes how the potential energy changes with bond bending. It was originally developed for pure Si, but has been extended to many other elements and compounds and also formed the basis for other Si potentials.

Metals are very commonly described with what can be called "EAM-like" potentials, i.e. potentials that share the same functional form as the embedded atom model. In these potentials, the total potential energy is written

where F i is a so-called embedding function (not to be confused with the force F → i ) that is a function of the sum of the so-called electron density ρ ( r i j ) . V 2 is a pair potential that usually is purely repulsive. In the original formulation the electron density function ρ ( r i j ) was obtained from true atomic electron densities, and the embedding function was motivated from density-functional theory as the energy needed to 'embed' an atom into the electron density. . However, many other potentials used for metals share the same functional form but motivate the terms differently, e.g. based on tight-binding theory or other motivations .

EAM-like potentials are usually implemented as numerical tables. A collection of tables is available at the interatomic potential repository at NIST [1]

Covalently bonded materials are often described by bond order potentials, sometimes also called Tersoff-like or Brenner-like potentials.

These have in general a form that resembles a pair potential:

where the repulsive and attractive part are simple exponential functions similar to those in the Morse potential. However, the strength is modified by the environment of the atom i via the b i j k term. If implemented without an explicit angular dependence, these potentials can be shown to be mathematically equivalent to some varieties of EAM-like potentials Thanks to this equivalence, the bond-order potential formalism has been implemented also for many metal-covalent mixed materials.

Repulsive potentials for short-range interactions

For very short interatomic separations, important in radiation material science, the interactions can be described quite accurately with screened Coulomb potentials which have the general form

here φ(r) → 1 when r → 0. Here Z 1 and Z 2 are the charges of the interacting nuclei, and a is the so-called screening parameter. A widely used popular screening function is the "Universal ZBL" one. and more accurate ones can be obtained from all-electron quantum chemistry calculations In binary collision approximation simulations this kind of potential can be used to describe the nuclear stopping power.

Potential fitting

Since the interatomic potentials are approximations, they by necessity all involve parameters that need to be adjusted to some reference values. In simple potentials such as the Lennard-Jones and Morse ones, the parameters can be set directly to match e.g. the equilibrium bond length and bond strength of a dimer molecule or the cohesive energy of a solid . However, many-body potentials often contain tens or even hundreds of adjustable parameters. These can be fit into a larger set of experimental data, or materials properties derived from more fundamental simulation models such as density-functional theory. For solids, a well-constructed many-body potential can often describe at least the equilibrium crystal structure cohesion and lattice constant, linear elastic constants, and basic point defect properties of all the elements and stable compounds well. . The aim of most potential construction and fitting is to make the potential transferable, i.e. that it can describe materials properties that are clearly different from those it was fitted to (for examples of potentials explicitly aiming for this, see e.g.). As an example of demonstrated partial transferability, a review of interatomic potentials of Si found that for instance the Stillinger-Weber and Tersoff III potentials for Si are indeed able to describe several (but certainly not all) materials properties they were not fitted to .

The NIST interatomic potential repository provides a collection of fitted interatomic potentials, either as fitted parameter values or numerical tables of the potential functions.

Reliability of interatomic potentials

Classical interatomic potentials cannot reproduce all phenomena. Sometimes quantum description is necessary. Density functional theory is used to overcome this limitation.