Incidence coloring

Definitions

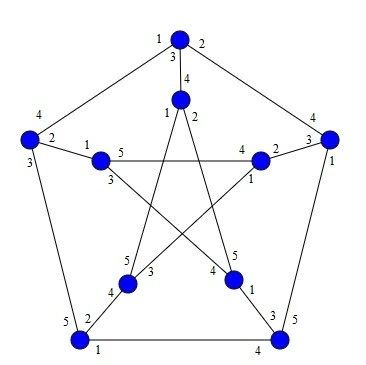
Let G = (V, E) be a simple graph with vertex set (non-empty) V(G) and edge set E(G). An incidence is defined as a pair (v, e) where v ϵ V(G) is an end point of e ϵ E(G). In simple words, one says that vertex v is incident to edge e.

Consider a set of incidences, say, I(G) = {(v,e) : v ϵ V(G) and e ϵ E(G) and v ϵ e}. The two incidences (v,e) and (u,f) are said to be adjacent if one of the given conditions holds:

An incidence coloring of G can be defined as a function c: I(G) → N such that c((v, e)) ≠ c((u,f)) for any incidences (v, e) and (u, f) that are adjacent. This implies that incidence coloring assigns distinct colors to neighborly incidences. [Generally, a simplified notation c(v, u) is used instead of c((v, e)).]

The minimum number of colors needed for incidence coloring of a graph is known as incidence chromatic number or incidence coloring number of G, represented by χ i (G). This notation was introduced by Jennifer J. Quinn Massey and Richard A. Brualdi in 1993.

Let A be a finite subset of N, the set of natural numbers. A is an interval if and only if it contains all the numbers between minimum of A and maximum of A. Consider c to be an incidence coloring of graph G. Let A c (v) = {c(v,e) : v is an end point of edge e where e belongs to edge set E(G)}. An interval incidence coloring of G is an incidence coloring c of graph G such that for each vertex v in V(G), the set A c (v) is an interval.

The interval incidence coloring number of G is the minimum number of colors used for the interval incidence coloring of G. It is denoted by IIC(G). If only IIC(G) colors are used for the interval incidence coloring, then it is said to be minimal.

History

The concept of incidence coloring was introduced by Brualdi and Massey in 1993. They bounded it in terms of Δ(G), the maximum degree of a graph G. Initially, the incidence chromatic number of trees, complete bipartite graphs and complete graphs was found out. They also conjectured that all graphs can have an incidence coloring using Δ(G) + 2 colors (Incidence coloring conjecture - ICC). This conjecture was disproved by Guiduli, who showed that incidence coloring concept is a directed star arboricity case, introduced by Alon and Algor. His counter example showed that incidence chromatic number is at most Δ(G) + O(log Δ(G)).

Chen et al. found the incidence chromatic number of paths, fans, cycles, wheels, complete tripartite graph and adding edge wheels. Few years later, Shiu et al. showed that this conjecture is true for certain cubic graphs such as cubic Hamiltonian graphs. He showed that in case of outerplanar graph of maximum degree 4, the incidence chromatic number is not 5. The bounds for incidence chromatic number of various graph classes is found out now.

Basic results

Consider a graph G with maximum degree Δ(G). The trivial lower bound for χ i (G) is given as: χ i (G) ≥ Δ(G) + 1.

Proof. Let v be the vertex with maximum degree Δ in G. Let e 1 , e 2 , e 3 , . . . , e Δ be the edges that are incident with the vertex v. Consider e 1 = { v,w }. We can see that every pair of Δ + 1 incidences, that is, ( v, e 1 ), ( v, e 2 ), ( v, e 3 ),......, ( v, e Δ ), ( w, e 1 ) is neighborly. Therefore, these incidences have to be colored using distinct colors.

The bound is attained by trees and complete graphs.

The main results were determined and proved by Brualdi and Massey(1993). Shiu, Sun and Wu have proposed certain necessary conditions for graph to meet the quality χ i (G) = Δ(G) + 1.

Meshes

Several algorithms are introduced to provide incidence coloring of meshes like square meshes, honeycomb meshes and hexagonal meshes. These algorithms are optimal. For each mesh, the incidence colors can be made in the linear time with the least number of colors. It is found out that Δ(G) + 1 colors are required for incidence coloring of square meshes, honeycomb meshes and hexagonal meshes.

Halin graphs

For a Halin graph G with maximum degree greater than 4, the incidence chromatic number is Δ(G) + 1; which was proved by Chen, Wang and Pang. In case of Halin graphs with Δ(G) = 3 or 4, Jing-Zhe Qu determined that the incidence chromatic number to be 5 or 6 respectively. If Halin graph G contains a tree T, then incidence chromatic number of H 2 is at most Δ( T 2 ) + Δ(T) + 8. Every cubic Halin graph other than complete graph on 4 vertices satisfies incidence coloring with Δ + 2 colors (Result proved by Shiu and Sun). Su, Meng and Guo extended this result and showed that all pseudo-Halin graphs satisfy incidence coloring conjecture. However, when the incidence coloring number of Halin graphs with low degree is Δ(G) + 1 colors is still an unsolved problem.

k-degenerated graphs

D.L. Chen, P.C.B. Lam and W.C. Shiu had conjectured that the incidence chromatic number of a cubic graph G is at most ∆(G)+2. They even proved that it is true in case of certain cubic graphs such as class of Hamiltonian cubic graphs. Based on these results, M. H. Dolama, E. Sopena and X. Zhu (2004) studied the graph classes for which χ i (G) is bounded by ∆(G) + c where c is some fixed constant. A graph is said to be k-generated if for every subgraph H of G, the minimum degree of H is at most k.

Outerplanar graphs

Consider an outerplanar graph G. Let vertex v in G be a cut vertex such that G – v is union of graphs H 1 and H 2 . Let graph G 1 be the induced subgraph on vertex v and vertices of H 1 ; and graph G 2 be the induced subgraph on vertex v and vertices of H 2 . Then incidence chromatic number of G is maximum among incidence chromatic number of G 1 , G 2 and 1 + d G (v) where d G (v) is the degree of vertex v in G.

The incidence chromatic number of an outerplanar graph G is at most Δ(G) + 2 where Δ(G) is maximum degree of G. In case of outerplanar graphs with Δ(G) greater than 3, the incidence chromatic number is Δ(G) +1.

Since outerplanar graphs are k₄-minor-free graphs, they accept a (Δ + 2, 2) – incidence coloring. The solution for incidence chromatic number of the outerplanar graph G having Δ(G) = 3 and 2-connected outerplanar graph is still an open question.

Chordal rings

Chordal rings are variations of ring networks. The use of chordal rings in communication is very extensive due to its advantages over the interconnection networks with ring topology and other analysed structures such as meshes, hypercubes, Cayley's graphs, etc. Arden and Lee first proposed the chordal ring of degree 3, that is, the ring structured network in which every node has an extra link known as chord, to some other node in the network. Distributed loop networks are chordal rings of degree 4 which is constructed by adding 2 extra chords at every vertex in a ring network.

Chordal rings, denoted by CR(N,d) is a graph with vertex set V(G) = { v 0 , v 1 , v 2 , . . . . , v N − 1 } and edge set E(G) = { v i v j : [ i − j ] N = 1 or d }, where [ x ] y denotes x modulo y, n is number of nodes and d is chord length. These graphs are studied due to its application in communication. Kung-Fu Ding, Kung-Jui Pai and Ro-Yu Wu studied the incidence coloring of chordal rings. Several algorithms are formulated to find the incidence chromatic number of chordal rings. The major findings are:

Powers of cycles

Keaitsuda Nakprasit and Kittikorn Nakprasit studied the incidence coloring of powers of cycles. They have proved that C n k except for certain cases, satisfies the (Δ + 2) conjecture where k is an integer. It was found out that χ i ( C n k ) = 2k + 1 = Δ( C n k ) + 1 when n is divisible by 2k + 1, else χ i ( C n k ) = 2k + 2. If n is divisible by 5, χ i ( C n 2 ) = 5. Otherwise, χ i ( C n 2 ) = 6. Apart from the powers of cycles, studies have been done on powers of other graphs too.

Relation between incidence chromatic number and domination number of a graph

Consider a simple connected graph G with order n, size m and domination number γ . Then, χ i (G) ≥ 2 m n − γ .

Proof. Form a digraph D(G) from graph G by dividing each edge of G into 2 arcs in opposite directions. We can see that the total number of arcs in D(G) is 2m. According to Guiduli, the incidence coloring of G is equivalent to proper coloring of the digraph D(G), where 2 distinct arcs u v → and x y → are adjacent if one of the following conditions holds: (i) u = x; (ii) v = x or y = u. By the definition of adjacency of arcs, an independent set of arcs in D(G) is a star forest. Therefore, a maximal independent set of arcs is a maximal star forest. This implies that at least 2 m n − γ color classes are required.

This relation has been widely used in the characterization of (r+1)-incidence colorable r-regular graphs. The major result on incidence coloring of r-regular graphs is: If graph G is r-regular graph, then χ i ( G ) = χ i ( G 2 ) = r + 1 if and only if V (G) is a disjoint union of r + 1 dominating sets.

Interval incidence coloring

The interval incidence coloring of graph G is an incidence coloring of G such that the set of colors given for the incidences adjoining the same vertex forms an interval. The interval incidence coloring number, denoted by χ i i is the smallest number of colors needed for an interval incidence coloring of G. It is clear that χ i (G) ≤ χ i i (G).

The concept of interval incidence coloring was introduced by A. Malafiejska, R. Janczewski and M. Malafiejski. They proved that χ i i (G) ≤ 2∆(G) for any bipartite graph G. In case of regular bipartite graphs, this equality holds. Subcubic bipartite graphs admit an interval incidence coloring using four, five or six colors. They have also proved that in linear time, for every bipartite graph with ∆(G) = 4, deciding interval incidence 5-colorability can be performed.

Fractional incidence coloring

The fractional version of the incidence coloring was first introduced by Yang in 2007. A r-tuple incidence k-coloring of a graph G is the assignment of r colors to each incidence of graph G from a set of k colors such that the neighboring (adjacent) incidences are given disjoint sets of colors. By definition, it is obvious that 1-tuple incidence k-coloring is an incidence k-coloring too.

The fractional incidence chromatic number of graph G is the infimum of the fractions k r in such a way that G admits a r-tuple incidence k-coloring. Fractional incidence coloring has great applications in several fields of computer science. Based on incidence coloring results by Guiduli, Yang has proved that the fractional incidence chromatic number of any graph having maximum degree ∆(G) is at most ∆(G) + 20 log ∆(G) + 84. He has also proved the existence of graphs with fractional incidence chromatic number at least ∆(G) + Ω(log ∆(G)).

Nordhaus–Gaddum inequality

The Nordhaus–Gaddum inequality has been developed for the incidence chromatic number χ i (G) of graph G. Consider a graph G with n vertices such that G ≠ K n or K n ¯ . Let G ¯ represents the complement graph of G. Then, n +2 ≤ χ i (G) + χ i ( G ¯ ) ≤ 2n − 1. These bounds are sharp for all values of n.

Incidence coloring game

Incidence coloring game was first introduced by S. D. Andres. It is the incidence version of the vertex coloring game, in which the incidences of a graph are colored instead of vertices. Incidence game chromatic number is the new parameter defined as a game-theoretic analogous of the incidence chromatic number.

The game is that two players, Alice and Bob construct a proper incidence coloring. The rules are stated below:

The incidence game chromatic number of a graph G, denoted by i g ( G ) , is the least number of colors required for Alice to win in incidence coloring game. It unifies the ideas of incidence chromatic number of a graph and game chromatic number in case of an undirected graph. Andres found out that the upper bound for i g ( G ) in case of k-degenerate graphs with maximum degree Δ is 2Δ + 4k - 2. This bound was improved to 2Δ + 3k - 1 in case of graphs in which Δ is at least 5k. The incidence game chromatic number of stars, cycles, and sufficiently large wheels are also determined. John Y. Kim (2011) has found out the exact incidence game chromatic number of large paths and has given a correct proof of a result stated by Andres concerning the exact incidence game chromatic number of large wheels.