Samiksha Jaiswal (Editor)

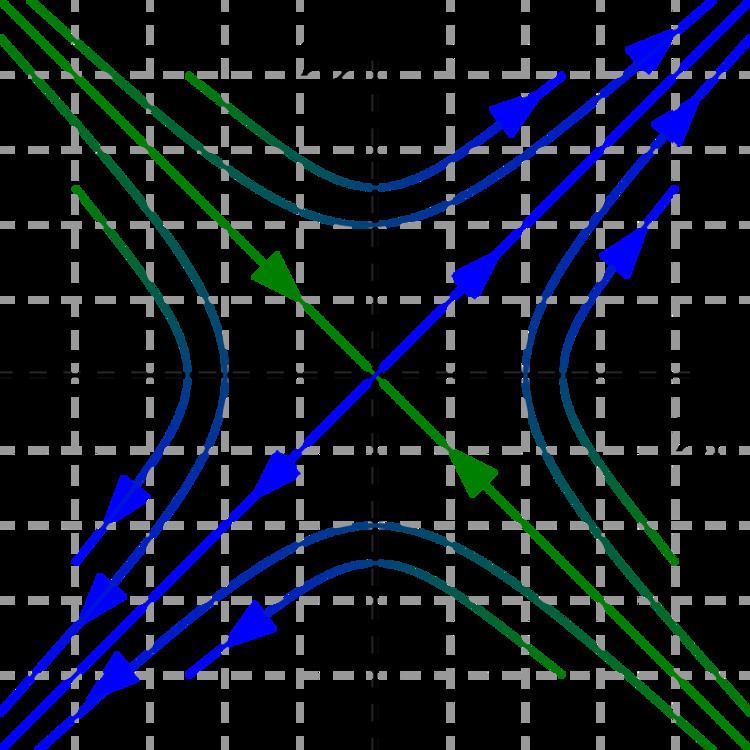
Hyperbolic equilibrium point

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Hyperbolic equilibrium point

In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name – it sounds like it should mean 'saddle point' – but it has become standard." Several properties hold about a neighborhood of a hyperbolic point, notably

Contents

  • A stable manifold and an unstable manifold exist,
  • Shadowing occurs,
  • The dynamics on the invariant set can be represented via symbolic dynamics,
  • A natural measure can be defined,
  • The system is structurally stable.

    • Maps

    If T : Rn → Rn is a C1 map and p is a fixed point then p is said to be a hyperbolic fixed point when the Jacobian matrix DT(p) has no eigenvalues on the unit circle.

    One example of a map that its only fixed point is hyperbolic is the Arnold Map or cat map:

    [ x n + 1 y n + 1 ] = [ 1 1 1 2 ] [ x n y n ]

    Since the eigenvalues are given by

    λ 1 = 3 + 5 2 > 1 λ 2 = 3 − 5 2 < 1

    Flows

    Let F : Rn → Rn be a C1 vector field with a critical point p, i.e., F(p) = 0, and let J denote the Jacobian matrix of F at p. If the matrix J has no eigenvalues with zero real parts then p is called hyperbolic. Hyperbolic fixed points may also be called hyperbolic critical points or elementary critical points.

    The Hartman-Grobman theorem states that the orbit structure of a dynamical system in a neighbourhood of a hyperbolic equilibrium point is topologically equivalent to the orbit structure of the linearized dynamical system.

    Example

    Consider the nonlinear system

    d x d t = y , d y d t = − x − x 3 − α y ,   α ≠ 0

    (0, 0) is the only equilibrium point. The linearization at the equilibrium is

    J ( 0 , 0 ) = ( 0 1 − 1 − α ) .

    The eigenvalues of this matrix are − α ± α 2 − 4 2 . For all values of α ≠ 0, the eigenvalues have non-zero real part. Thus, this equilibrium point is a hyperbolic equilibrium point. The linearized system will behave similar to the non-linear system near (0, 0). When α = 0, the system has a nonhyperbolic equilibrium at (0, 0).

    Comments

    In the case of an infinite dimensional system - for example systems involving a time delay - the notion of the "hyperbolic part of the spectrum" refers to the above property.

    References

    Hyperbolic equilibrium point Wikipedia
    (Text) CC BY-SA