 | ||
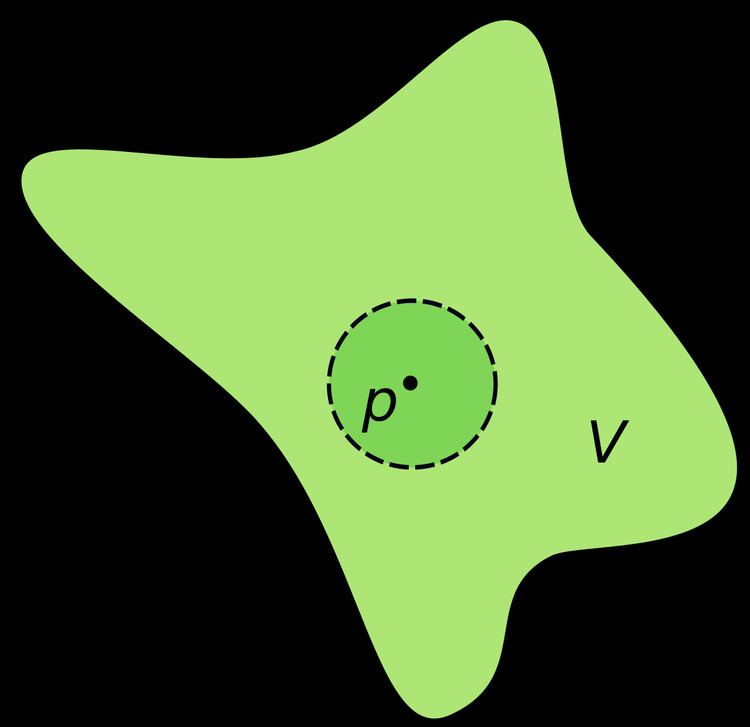
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and interior. Intuitively speaking, a neighbourhood of a point is a set of points containing that point where one can move some amount away from that point without leaving the set.
Contents
Neighbourhood of a point
If
This is also equivalent to
Note that the neighbourhood
A set that is a neighbourhood of each of its points is open since it can be expressed as the union of open sets containing each of its points. A rectangle, as illustrated in the figure, is not a neighbourhood of all its points; points on the edges or corners of the rectangle are not contained in any open set that is contained within the rectangle.
The collection of all neighbourhoods of a point is called the neighbourhood system at the point.
Neighbourhood of a set
If
In a metric space
In a metric space
is contained in
is contained in
For
It directly follows that an
Examples
Given the set of real numbers
then
Topology from neighbourhoods
The above definition is useful if the notion of open set is already defined. There is an alternative way to define a topology, by first defining the neighbourhood system, and then open sets as those sets containing a neighbourhood of each of their points.
A neighbourhood system on
- the point
x is an element of eachU inN ( x ) - each
U inN ( x ) contains someV inN ( x ) such that for eachy inV ,U is inN ( y ) .
One can show that both definitions are compatible, i.e. the topology obtained from the neighbourhood system defined using open sets is the original one, and vice versa when starting out from a neighbourhood system.
Uniform neighbourhoods
In a uniform space
Deleted neighbourhood
A deleted neighbourhood of a point
