Supriya Ghosh (Editor)

Compatibility (mechanics)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Compatibility (mechanics)

In continuum mechanics, a compatible deformation (or strain) tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

Contents

In the continuum description of a solid body we imagine the body to be composed of a set of infinitesimal volumes or material points. Each volume is assumed to be connected to its neighbors without any gaps or overlaps. Certain mathematical conditions have to be satisfied to ensure that gaps/overlaps do not develop when a continuum body is deformed. A body that deforms without developing any gaps/overlaps is called a compatible body. Compatibility conditions are mathematical conditions that determine whether a particular deformation will leave a body in a compatible state.

In the context of infinitesimal strain theory, these conditions are equivalent to stating that the displacements in a body can be obtained by integrating the strains. Such an integration is possible if the Saint-Venant's tensor (or incompatibility tensor) R ( ε ) vanishes in a simply-connected body where ε is the infinitesimal strain tensor and

R := ∇ × ( ∇ × ε )   .

For finite deformations the compatibility conditions take the form

R := ∇ × F = 0

where F is the deformation gradient.

Compatibility conditions for infinitesimal strains

The compatibility conditions in linear elasticity are obtained by observing that there are six strain-displacement relations that are functions of only three unknown displacements. This suggests that the three displacements may be removed from the system of equations without loss of information. The resulting expressions in terms of only the strains provide constraints on the possible forms of a strain field.

2-dimensions

For two-dimensional, plane strain problems the strain-displacement relations are

ε 11 = ∂ u 1 ∂ x 1   ;     ε 12 = 1 2 [ ∂ u 1 ∂ x 2 + ∂ u 2 ∂ x 1 ]   ;     ε 22 = ∂ u 2 ∂ x 2

Combining these relations gives us the two-dimensional compatibility condition for strains

∂ 2 ε 11 ∂ x 2 2 − 2 ∂ 2 ε 12 ∂ x 1 ∂ x 2 + ∂ 2 ε 22 ∂ x 1 2 = 0

The only displacement field that is allowed by a compatible plane strain field is a plane displacement field, i.e., u = u ( x 1 , x 2 ) .

3-dimensions

In three dimensions, in addition to two more equations of the form seen for two dimensions, there are three more equations of the form

∂ 2 ε 33 ∂ x 1 ∂ x 2 = ∂ ∂ x 3 [ ∂ ε 23 ∂ x 1 + ∂ ε 31 ∂ x 2 − ∂ ε 12 ∂ x 3 ]

Therefore there are 34=81 partial differential equations however due to symmetry conditions this number reduces to six different compatibility conditions. We can write these conditions in index notation as

e i k r   e j l s   ε i j , k l = 0

where e i j k is the permutation symbol. In direct tensor notation

∇ × ( ∇ × ε ) = 0

where the curl operator can be expressed in an orthonormal coordinate system as ∇ × ε = e i j k ε r j , i e k ⊗ e r .

The second-order tensor

R := ∇ × ( ∇ × ε )   ;     R r s := e i k r   e j l s   ε i j , k l

is known as the incompatibility tensor, and is equivalent to the Saint-Venant compatibility tensor

Compatibility conditions for finite strains

For solids in which the deformations are not required to be small, the compatibility conditions take the form

∇ × F = 0

where F is the deformation gradient. In terms of components with respect to a Cartesian coordinate system we can write these compatibility relations as

e A B C   ∂ F i B ∂ X A = 0

This condition is necessary if the deformation is to be continuous and derived from the mapping x = χ ( X , t ) (see Finite strain theory). The same condition is also sufficient to ensure compatibility in a simply connected body.

Compatibility condition for the right Cauchy-Green deformation tensor

The compatibility condition for the right Cauchy-Green deformation tensor can be expressed as

R α β ρ γ := ∂ ∂ X ρ [ Γ α β γ ] − ∂ ∂ X β [ Γ α ρ γ ] + Γ μ ρ γ   Γ α β μ − Γ μ β γ   Γ α ρ μ = 0

where Γ i j k is the Christoffel symbol of the second kind. The quantity R i j k m represents the mixed components of the Riemann-Christoffel curvature tensor.

The general compatibility problem

The problem of compatibility in continuum mechanics involves the determination of allowable single-valued continuous fields on simply connected bodies. More precisely, the problem may be stated in the following manner.

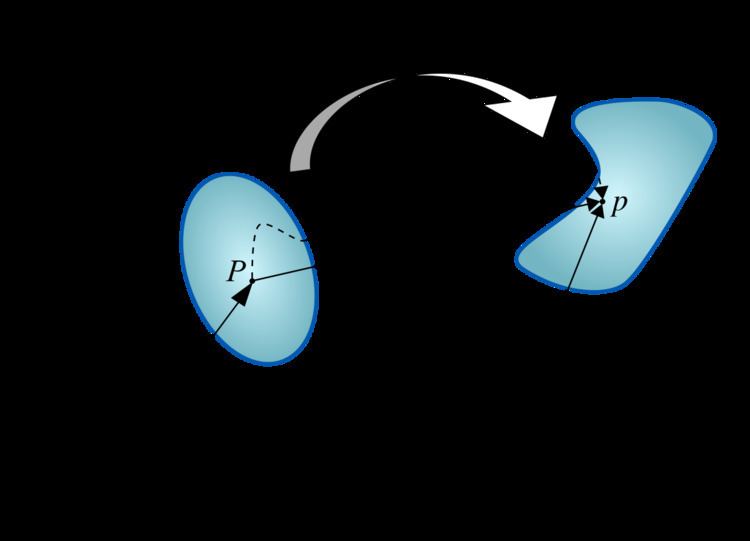
Consider the deformation of a body shown in Figure 1. If we express all vectors in terms of the reference coordinate system { ( E 1 , E 2 , E 3 ) , O } , the displacement of a point in the body is given by

u = x − X   ;     u i = x i − X i

Also

∇ u = ∂ u ∂ X   ;     ∇ x = ∂ x ∂ X

What conditions on a given second-order tensor field A ( X ) on a body are necessary and sufficient so that there exists a unique vector field v ( X ) that satisfies

∇ v = A ≡ v i , j = A i j

Necessary conditions

For the necessary conditions we assume that the field v exists and satisfies v i , j = A i j . Then

v i , j k = A i j , k   ;     v i , k j = A i k , j

Since changing the order of differentiation does not affect the result we have

v i , j k = v i , k j

Hence

A i j , k = A i k , j

From the well known identity for the curl of a tensor we get the necessary condition

∇ × A = 0

Sufficient conditions

To prove that this condition is sufficient to guarantee existence of a compatible second-order tensor field, we start with the assumption that a field A exists such that ∇ × A = 0 . We will integrate this field to find the vector field v along a line between points A and B (see Figure 2), i.e.,

v ( X B ) − v ( X A ) = ∫ X A X B ∇ v ⋅   d X = ∫ X A X B A ( X ) ⋅ d X

If the vector field v is to be single-valued then the value of the integral should be independent of the path taken to go from A to B .

From Stokes theorem, the integral of a second order tensor along a closed path is given by

∮ ∂ Ω A   d s = ∫ Ω n ⋅ ( ∇ × A )   d a

Using the assumption that the curl of A is zero, we get

∮ ∂ Ω A   d s = 0 ⟹ ∫ A B A ⋅ d X + ∫ B A A ⋅ d X = 0

Hence the integral is path independent and the compatibility condition is sufficient to ensure a unique v field, provided that the body is simply connected.

Compatibility of the deformation gradient

The compatibility condition for the deformation gradient is obtained directly from the above proof by observing that

F = ∂ x ∂ X = ∇ x

Then the necessary and sufficient conditions for the existence of a compatible F field over a simply connected body are

∇ × F = 0

Compatibility of infinitesimal strains

The compatibility problem for small strains can be stated as follows.

Given a symmetric second order tensor field ϵ when is it possible to construct a vector field u such that

ϵ = 1 2 [ ∇ u + ( ∇ u ) T ]

Necessary conditions

Suppose that there exists u such that the expression for ϵ holds. Now

∇ u = ϵ + ω

where

ω := 1 2 [ ∇ u − ( ∇ u ) T ]

Therefore, in index notation,

∇ ω ≡ ω i j , k = 1 2 ( u i , j k − u j , i k ) = 1 2 ( u i , j k + u k , j i − u j , i k − u k , j i ) = ε i k , j − ε j k , i

If ω is continuously differentiable we have ω i j , k l = ω i j , l k . Hence,

ε i k , j l − ε j k , i l − ε i l , j k + ε j l , i k = 0

In direct tensor notation

∇ × ( ∇ × ϵ ) = 0

The above are necessary conditions. If w is the infinitesimal rotation vector then ∇ × ϵ = ∇ w + ∇ w T . Hence the necessary condition may also be written as ∇ × ( ∇ w + ∇ w T ) = 0 .

Sufficient conditions

Let us now assume that the condition ∇ × ( ∇ × ϵ ) = 0 is satisfied in a portion of a body. Is this condition sufficient to guarantee the existence of a continuous, single-valued displacement field u ?

The first step in the process is to show that this condition implies that the infinitesimal rotation tensor ω is uniquely defined. To do that we integrate ∇ w along the path X A to X B , i.e.,

w ( X B ) − w ( X A ) = ∫ X A X B ∇ w ⋅ d X = ∫ X A X B ( ∇ × ϵ ) ⋅ d X

Note that we need to know a reference w ( X A ) to fix the rigid body rotation. The field w ( X ) is uniquely determined only if the contour integral along a closed contour between X A and X b is zero, i.e.,

∮ X A X B ( ∇ × ϵ ) ⋅ d X = 0

But from Stokes' theorem for a simply-connected body and the necessary condition for compatibility

∮ X A X B ( ∇ × ϵ ) ⋅ d X = ∫ Ω A B n ⋅ ( ∇ × ∇ × ϵ )   d a = 0

Therefore the field w is uniquely defined which implies that the infinitesimal rotation tensor ω is also uniquely defined, provided the body is simply connected.

In the next step of the process we will consider the uniqueness of the displacement field u . As before we integrate the displacement gradient

u ( X B ) − u ( X A ) = ∫ X A X B ∇ u ⋅ d X = ∫ X A X B ( ϵ + ω ) ⋅ d X

From Stokes' theorem and using the relations ∇ × ϵ = ∇ w = − ∇ × Ω we have

∮ X A X B ( ϵ + ω ) ⋅ d X = ∫ Ω A B n ⋅ ( ∇ × ϵ + ∇ × ω )   d a = 0

Hence the displacement field u is also determined uniquely. Hence the compatibility conditions are sufficient to guarantee the existence of a unique displacement field u in a simply-connected body.

Compatibility for Right Cauchy-Green Deformation field

The compatibility problem for the Right Cauchy-Green deformation field can be posed as follows.

Problem: Let C ( X ) be a positive definite symmetric tensor field defined on the reference configuration. Under what conditions on C does there exist a deformed configuration marked by the position field x ( X ) such that

( 1 ) ( ∂ x ∂ X ) T ( ∂ x ∂ X ) = C

Necessary conditions

Suppose that a field x ( X ) exists that satisfies condition (1). In terms of components with respect to a rectangular Cartesian basis

∂ x i ∂ X α ∂ x i ∂ X β = C α β

From finite strain theory we know that C α β = g α β . Hence we can write

δ i j   ∂ x i ∂ X α   ∂ x j ∂ X β = g α β

For two symmetric second-order tensor field that are mapped one-to-one we also have the relation

G i j = ∂ X α ∂ x i   ∂ X β ∂ x j   g α β

From the relation between of G i j and g α β that δ i j = G i j , we have

( x ) Γ i j k = 0

Then, from the relation

∂ 2 x m ∂ X α ∂ X β = ∂ x m ∂ X μ ( X ) Γ α β μ − ∂ x i ∂ X α   ∂ x j ∂ X β ( x ) Γ i j m

we have

∂ F   α m ∂ X β = F   μ m ( X ) Γ α β μ ;     F   α i := ∂ x i ∂ X α

From finite strain theory we also have

( X ) Γ α β γ = 1 2 ( ∂ g α γ ∂ X β + ∂ g β γ ∂ X α − ∂ g α β ∂ X γ )   ;     ( X ) Γ α β ν = g ν γ ( X ) Γ α β γ   ;     g α β = C α β   ;     g α β = C α β

Therefore

( X ) Γ α β μ = C μ γ 2 ( ∂ C α γ ∂ X β + ∂ C β γ ∂ X α − ∂ C α β ∂ X γ )

and we have

∂ F   α m ∂ X β = F   μ m   C μ γ 2 ( ∂ C α γ ∂ X β + ∂ C β γ ∂ X α − ∂ C α β ∂ X γ )

Again, using the commutative nature of the order of differentiation, we have

∂ 2 F   α m ∂ X β ∂ X ρ = ∂ 2 F   α m ∂ X ρ ∂ X β ⟹ ∂ F   μ m ∂ X ρ ( X ) Γ α β μ + F   μ m   ∂ ∂ X ρ [ ( X ) Γ α β μ ] = ∂ F   μ m ∂ X β ( X ) Γ α ρ μ + F   μ m   ∂ ∂ X β [ ( X ) Γ α ρ μ ]

or

F   γ m ( X ) Γ μ ρ γ ( X ) Γ α β μ + F   μ m   ∂ ∂ X ρ [ ( X ) Γ α β μ ] = F   γ m ( X ) Γ μ β γ ( X ) Γ α ρ μ + F   μ m   ∂ ∂ X β [ ( X ) Γ α ρ μ ]

After collecting terms we get

F   γ m ( ( X ) Γ μ ρ γ ( X ) Γ α β μ + ∂ ∂ X ρ [ ( X ) Γ α β γ ] − ( X ) Γ μ β γ ( X ) Γ α ρ μ − ∂ ∂ X β [ ( X ) Γ α ρ γ ] ) = 0

From the definition of F γ m we observe that it is invertible and hence cannot be zero. Therefore,

R α β ρ γ := ∂ ∂ X ρ [ ( X ) Γ α β γ ] − ∂ ∂ X β [ ( X ) Γ α ρ γ ] + ( X ) Γ μ ρ γ ( X ) Γ α β μ − ( X ) Γ μ β γ ( X ) Γ α ρ μ = 0

We can show these are the mixed components of the Riemann-Christoffel curvature tensor. Therefore the necessary conditions for C -compatibility are that the Riemann-Christoffel curvature of the deformation is zero.

Sufficient conditions

The proof of sufficiency is a bit more involved. We start with the assumption that

R α β ρ γ = 0   ;     g α β = C α β

We have to show that there exist x and X such that

∂ x i ∂ X α ∂ x i ∂ X β = C α β

From a theorem by T.Y.Thomas we know that the system of equations

∂ F   α i ∂ X β = F   γ i   ( X ) Γ α β γ

has unique solutions F   α i over simply connected domains if

( X ) Γ α β γ = ( X ) Γ β α γ   ;     R α β ρ γ = 0

The first of these is true from the defining of Γ j k i and the second is assumed. Hence the assumed condition gives us a unique F   α i that is C 2 continuous.

Next consider the system of equations

∂ x i ∂ X α = F   α i

Since F   α i is C 2 and the body is simply connected there exists some solution x i ( X α ) to the above equations. We can show that the x i also satisfy the property that

det | ∂ x i ∂ X α | ≠ 0

We can also show that the relation

∂ x i ∂ X α   g α β   ∂ x j ∂ X β = δ i j

implies that

g α β = C α β = ∂ x k ∂ X α   ∂ x k ∂ X β

If we associate these quantities with tensor fields we can show that ∂ x ∂ X is invertible and the constructed tensor field satisfies the expression for C .

References

Compatibility (mechanics) Wikipedia
(Text) CC BY-SA


Similar Topics