Suvarna Garge (Editor)

Blasius boundary layer

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Blasius boundary layer

In physics and fluid mechanics, a Blasius boundary layer (named after Paul Richard Heinrich Blasius) describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

Contents

Prandtl's boundary layer equations

Using scaling arguments, Ludwig Prandtl has argued that about half of the terms in the Navier-Stokes equations are negligible in boundary layer flows (except in a small region near the leading edge of the plate). This leads to a reduced set of equations knows as the boundary layer equations. For steady incompressible flow with constant viscosity and density, these read:

Continuity: ∂ u ∂ x + ∂ v ∂ y = 0

x -Momentum: u ∂ u ∂ x + v ∂ u ∂ y = − 1 ρ ∂ p ∂ x + ν ∂ 2 u ∂ y 2

y -Momentum: ∂ p ∂ y = 0

Here the coordinate system is chosen with x pointing parallel to the plate in the direction of the flow and the y coordinate pointing towards the free stream, u and v are the x and y velocity components, p is the pressure, ρ is the density and ν is the kinematic viscosity.

These three partial differential equations for u , v and p can be reduced to a single equation for u as follows

  • By integrating the continuity equation over y , v can be expressed as a function of u :

    • v = − ∫ ∂ u ∂ x d y

  • The y -momentum equation implies that the pressure in the boundary layer must be equal to that of the free stream for any given x coordinate. Because the velocity profile is flat in the free stream, there are no viscous effects and Bernoulli's law applies:


    • p ρ + U ∞ 2 2 = constant


    or, after differentiation:


    1 ρ d p d x = − U ∞ d U ∞ d x

    Here U ∞ is the velocity of the free stream. The derivatives are not partials because there is no variation with respect to the y coordinate.

    Substitution of these results into the x -momentum equations gives:

    u ∂ u ∂ x − ∂ u ∂ y ∫ ∂ u ∂ x d y = U ∞ d U ∞ d x + ν ∂ 2 u ∂ y 2

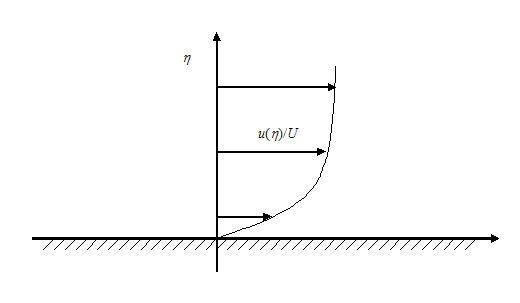
    A number of similarity solutions to this equation have been found for various types of flow, including flat plate boundary layers. The term similarity refers to the property that the velocity profiles at different positions in the flow are the same apart from a scaling factor. These solutions are often presented in the form of non-linear ordinary differential equations.

    Blasius equation

    Blasius proposed a similarity solution for the case in which the free stream velocity is constant, ∂ U / ∂ x = 0 , which corresponds to the boundary layer over a flat plate that is oriented parallel to the free flow. First he introduced the similarity variable

    η = y δ ( x ) = y U 2 ν x

    Where δ ( x ) = 2 ν x / U is proportional to the boundary layer thickness. The factor 2 is actually a later addition that, as White points out, avoids a constant in the final differential equation. Next Blasius proposed the stream function

    ψ = 2 ν U x f ( η )

    in which the newly introduced normalized stream function, f ( η ) , is only a function of the similarity variable. This leads directly to the velocity components

    u ( x , y ) = ∂ ψ ∂ y = U f ′ ( η ) v ( x , y ) = − ∂ ψ ∂ x = ν U 2 x ( η f ′ − f )

    Where the prime denotes derivation with respect to η . Substitution into the momentum equation gives the Blasius equation

    f ‴ + f ″ f = 0

    This is a third order non-linear ordinary differential equation which can be solved numerically, e.g. with the shooting method.

    The boundary conditions are the no-slip condition

    u ( x , 0 ) = 0 → f ′ ( 0 ) = 0

    impermeability of the wall

    v ( x , 0 ) = 0 → f ( 0 ) = 0

    and the free stream velocity outside the boundary layer

    u ( x , ∞ ) = U → f ′ ( ∞ ) = 1

    Falkner–Skan equation

    We can generalize the Blasius boundary layer by considering a wedge at an angle of attack π β / 2 from some uniform velocity field U 0 . We then estimate the outer flow to be of the form:

    u e ( x ) = U 0 ( x L ) m

    Where L is a characteristic length and m is a dimensionless constant. In the Blasius solution, m = 0 corresponding to an angle of attack of zero radians. Thus we can write:

    β = 2 m m + 1 .

    As in the Blasius solution, we use a similarity variable η to solve the boundary layer equations.

    η = y U 0 ( m + 1 ) 2 ν L ( x L ) ( m − 1 ) / 2

    It becomes easier to describe this in terms of its stream function which we write as

    ψ = U ( x ) δ ( x ) f ( η ) = 2 ν U 0 L m + 1 ( x L ) ( m + 1 ) / 2 f ( η )

    Thus the initial differential equation which was written as follows:

    u ∂ u ∂ x + v ∂ u ∂ y = c 2 m x 2 m − 1 + ν ∂ 2 u ∂ y 2 .

    Can now be expressed in terms of the non-linear ODE known as the Falkner–Skan equation (named after V. M. Falkner and Sylvia W. Skan).

    f ‴ + f f ″ + β [ 1 − ( f ′ ) 2 ] = 0

    Here, m < 0 corresponds to an adverse pressure gradient (often resulting in boundary layer separation) while m > 0 represents a favorable pressure gradient. (Note that m = 0 recovers the Blasius equation). In 1937 Douglas Hartree showed that physical solutions to the Falkner–Skan equation exist only in the range -0.0905 ≤ m ≤ 2. For more negative values of m, that is, for stronger adverse pressure gradients, all solutions satisfying the boundary conditions at η = 0 have the property that f(η) > 1 for a range of values of η. This is physically unacceptable because it implies that the velocity in the boundary layer is greater than in the main flow.

    Further details may be found in Wilcox (2007).

    References

    Blasius boundary layer Wikipedia
    (Text) CC BY-SA