 | ||
Biogeography-based optimization (BBO) is an evolutionary algorithm (EA) that optimizes a function by stochastically and iteratively improving candidate solutions with regard to a given measure of quality, or fitness function. BBO belongs to the class of metaheuristics since it includes many variations, and since it does not make any assumptions about the problem and can therefore be applied to a wide class of problems.
Contents
- Underlying principles
- Algorithm
- Discussion of the BBO algorithm
- Algorithmic variations
- Hybridization
- MATLAB
- R
- Extensions
- Mathematical analyses
- Applications
- References
BBO is typically used to optimize multidimensional real-valued functions, but it does not use the gradient of the function, which means that it does not require the function to be differentiable as required by classic optimization methods such as gradient descent and quasi-newton methods. BBO can therefore be used on discontinuous functions.
BBO optimizes a problem by maintaining a population of candidate solutions, and creating new candidate solutions by combining existing ones according to a simple formula. In this way the objective function is treated as a black box that merely provides a measure of quality given a candidate solution, and the function's gradient is not needed.
Like many EAs, BBO was motivated by a natural process; in particular, BBO was motivated by biogeography, which is the study of the distribution of biological species through time and space. BBO was originally introduced by Dan Simon in 2008.
Underlying principles
Mathematical models of biogeography describe speciation (the evolution of new species), the migration of species (animals, fish, birds, or insects) between islands, and the extinction of species. Islands that are friendly to life are said to have a high habitat suitability index (HSI). Features that correlate with HSI include rainfall, vegetative diversity, topographic diversity, land area, temperature, and others. The features that determine are called suitability index variables (SIVs). In terms of habitability, SIVs are the independent variables and HSI is the dependent variable.
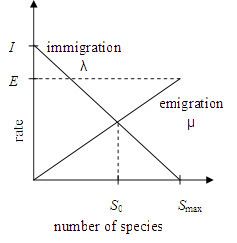
Islands with a high HSI can support many species, and islands with a low HSI can support only a few species. Islands with a high HSI have many species that emigrate to nearby habitats because of the large populations and the large numbers of species that they host. Note that emigration from an island with a high HSI does not occur because species want to leave their home; after all, their home island is an attractive place to live. Emigration occurs because of the accumulation of random effects on a large number of species with large populations. Emigration occurs as animals ride flotsam, swim, fly, or ride the wind to neighboring islands. When a species emigrates from an island, it does not mean that the species completely disappears from its original island; only a few representatives emigrate, so an emigrating species remains present on its original island while at the same time migrating to a neighboring island. However, in BBO it is assumed that emigration from an island results in extinction from that island. This assumption is necessary in BBO because species represent the independent variables of a function, and each island represents a candidate solution to a function optimization problem.
Islands with a high HSI not only have a high emigration rate, but they also have a low immigration rate because they already support many species. Species that migrate to such islands will tend to die in spite of the island's high HSI, because there is too much competition for resources from other species.
Islands with a low HSI have a high immigration rate because of their low populations. Again, this is not because species want to immigrate to such islands; after all, these islands are undesirable places to live. The reason that immigration occurs to these islands is because there is a lot of room for additional species. Whether or not the immigrating species can survive in its new home, and for how long, is another question. However, species diversity is correlated with HSI, so when more species arrive at a low HSI island, the island's HSI will tend to increase.
The figure on the right illustrates an island migration model. The immigration rate
In BBO,
for
Algorithm
Like most other EAs, BBO includes mutation. A basic BBO algorithm with a population size of
Initialize a population of N candidate solutions { x k } While not(termination criterion) For each x k , set emigration probability μ k ∝ fitness of x k , with μ k ∈ [ 0 , 1 ] For each x k , set immigration probability λ k = 1 − μ k { z k } ← { x k } For each individual z k ( k = 1 , ⋯ , N ) For each independent variable index s ∈ [ 1 , n ] Use λ k to probabilistically decide whether to immigrate to z k If immigrating then Use { μ i } to probabilistically select the emigrating individual x j z k ( s ) ← x j ( s ) End if Next independent variable index: s ← s + 1 Probabilistically mutate z k Next individual: k ← k + 1 { x k } ← { z k } Next generationDiscussion of the BBO algorithm
Algorithmic variations
Many variations have been proposed to the basic BBO algorithm, among which are the following.
Hybridization
MATLAB
R
Extensions
BBO has been extended to noisy functions (that is, functions whose fitness evaluation is corrupted by noise); constrained functions; combinatorial functions; and multi-objective functions.
Mathematical analyses
BBO has been mathematically analyzed using Markov models and dynamic system models.
Applications
Scholars have applied BBO into various academic and industrial applications. They found BBO performed better than state-of-the-art global optimization methods.
For example, Wang et al. proved BBO performed equal performance with FSCABC but with simpler codes.
Yang et al. showed BBO was superior to GA, PSO, and ABC.
