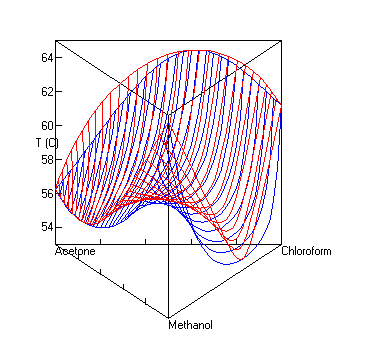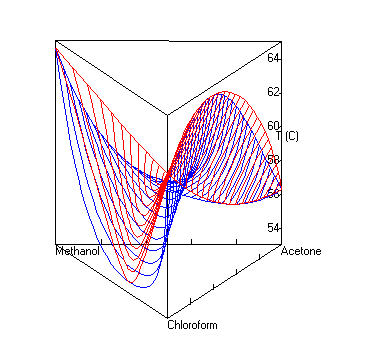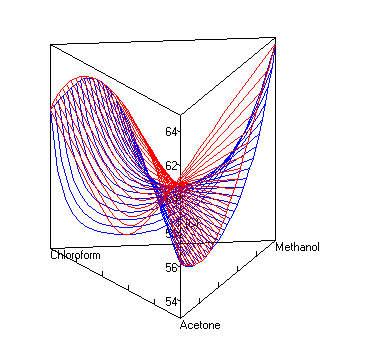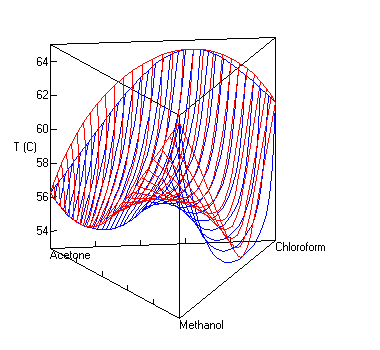
 | ||
The UNIFAC method (UNIQUAC Functional-group Activity Coefficients) is a semi-empirical system for the prediction of non-electrolyte activity in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients. By using interactions for each of the functional groups present on the molecules, as well as some binary interaction coefficients, the activity of each of the solutions can be calculated. This information can be used to obtain information on liquid equilibria, which is useful in many thermodynamic calculations, such as chemical reactor design, and distillation calculations.
Contents
The UNIFAC model was first published in 1975 by Fredenslund, Jones and Prausnitz, a group of chemical engineering researchers from the University of California. Subsequently they and other authors have published a wide range of UNIFAC papers, extending the capabilities of the model; this has been by the development of new or revision of existing UNIFAC model parameters. UNIFAC is an attempt by these researchers to provide a flexible liquid equilibria model for wider use in chemistry, the chemical and process engineering disciplines.
Introduction
A particular problem in the area of liquid-state thermodynamics is the sourcing of reliable thermodynamic constants. These constants are necessary for the successful prediction of the free energy state of the system; without this information it is impossible to model the equilibrium phases of the system.
Obtaining this free energy data is not a trivial problem, and requires careful experiments, such as calorimetry, to successfully measure the energy of the system. Even when this work is performed it is infeasible to attempt to conduct this work for every single possible class of chemicals, and the binary, or higher, mixtures thereof. To alleviate this problem, free energy prediction models, such as UNIFAC, are employed to predict the system's energy based on a few previously measured constants.
Although it is theoretically possible to calculate some of these parameters using ab initio methods like COSMO-RS, several major problems with this approach exist; firstly, and most importantly, the computational resources for such calculations are immense - scaling extremely unfavourably for systems with more than a few atoms. Secondly the energies obtained from these calculations obtained from ab initio simulations often require experimental verification to confirm their results. Finally such calculations require a significant level of expertise and a good understanding of quantum chemistry. Thus the need for simplified models that still successfully predict the thermodynamic state of the system, such as UNIFAC.
UNIFAC Correlation
The UNIFAC correlation attempts to break down the problem of predicting interactions between molecules by describing molecular interactions based upon the functional groups attached to the molecule. This is done in order to reduce the sheer number of binary interactions that would be needed to be measured to predict the state of the system.
Chemical Activity
The activity coefficient of the components in a system is a correction factor that accounts for deviations of real systems from that of an Ideal solution, which can either be measured via experiment or estimated from chemical models (such as UNIFAC). By adding a correction factor, known as the activity (
Equipped with the activity coefficients and a knowledge of the constituents and their relative amounts, phenomena such as phase separation and vapour-liquid equilibria can be calculated. UNIFAC attempts to be a general model for the successful prediction of activity coefficients.
Model Parameters
The UNIFAC model splits up the activity coefficient for each species in the system into two components; a combinatorial
In the UNIFAC model, there are three main parameters required to determine the activity for each molecule in the system. Firstly there are the group surface area
Combinatorial
The combinatorial component of the activity is contributed to by several terms in its equation (below), and is the same as for the UNIQUAC model.
Residual
The residual component of the activity
where
In this formula
Thus
