 | ||
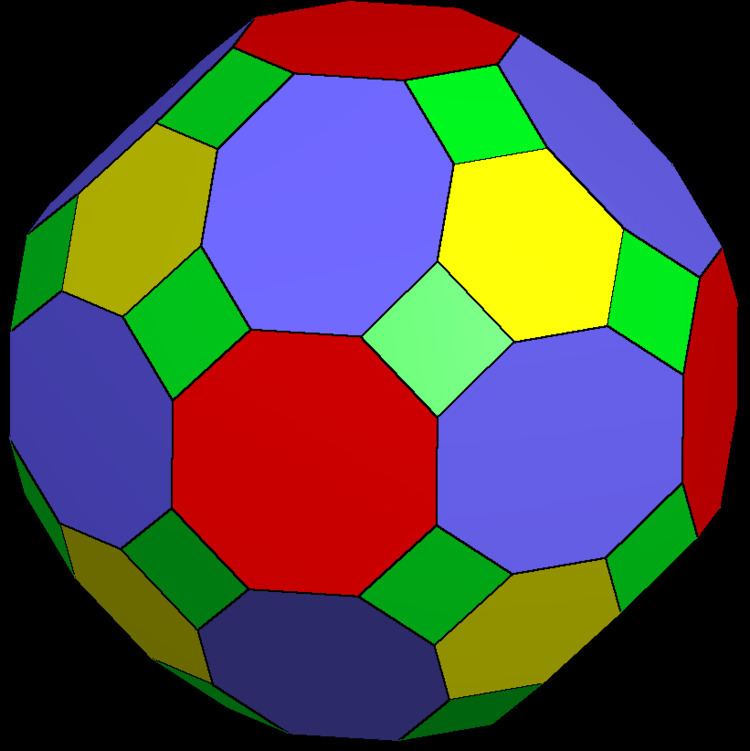
The truncated rhombicuboctahedron is a polyhedron, constructed as a truncated rhombicuboctahedron. It has 50 faces, 18 octagons, 8 hexagons, and 24 squares.
Contents
Other names
Zonohedron
As a zonohedron, it can be constructed with all but 12 octagons as regular polygons. It is has two sets of 48 vertices existing on two distances from its center.
It represents the Minkowski sum of a cube, a truncated octahedron, and a rhombic dodecahedron.
Excavated truncated rhombicuboctahedron
The truncated rhombicuboctahedron can have its 12 irregular octagonal faces removed, and a toroidal polyhedron seen as a network of 6 square cupolae, 8 triangular cupolae, and 24 triangular prisms. It has 148 faces (8 triangles, 126 squares, 8 hexagons, and 6 octagons), 312 edges, and 144 vertices. With Euler characteristic χ = f + v - e = -20, its genus, g = (2-χ)/2 is 11.
Without the triangular prisms, the toroidal polyhedron becomes a truncated cuboctahedron.
Related polyhedra
The truncated cuboctahedron is similar, with all regular faces, and 4.6.8 vertex figure.
The triangle and squares of the rhombicuboctahedron can be independently rectified or truncated, creating four permutations of polyhedra. The partially truncated forms can be seen as edge contractions of the truncated form.
The truncated rhombicuboctahedron can be seen in sequence of rectification and truncation operations from the cuboctahedron. A further alternation step leads to the snub rhombicuboctahedron.
