Type JohnsonJ3 - J4 - J5 Vertices 12 Symmetry group C4v, [4], (*44) | Edges 20 Vertex configuration 8(3.4.8)4(3.4) | |
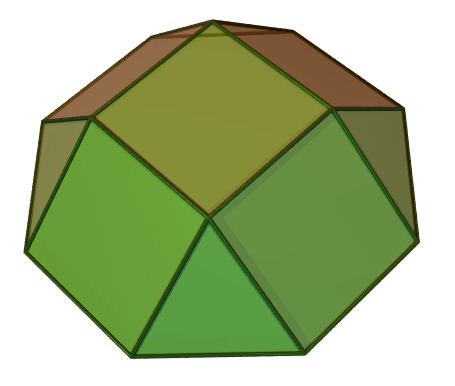 | ||
Faces 4 triangles1+4 squares1 octagon | ||
In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids (J4). It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagon.
Contents
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Formulae
The following formulae for volume, surface area, and circumradius can be used if all faces are regular, with edge length a:
Dual polyhedron
The dual of the square cupola has 8 triangular and 4 kite faces:
Crossed square cupola
The crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron, analogously to how the square cupola may be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.
It may be seen as a cupola with a retrograde square base, so that the squares and triangles connect across the bases in the opposite way to the square cupola, hence intersecting each other.
Honeycombs
The square cupola is a component of several nonuniform space-filling lattices:
