 | ||
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Contents
Definitions – theme and variations
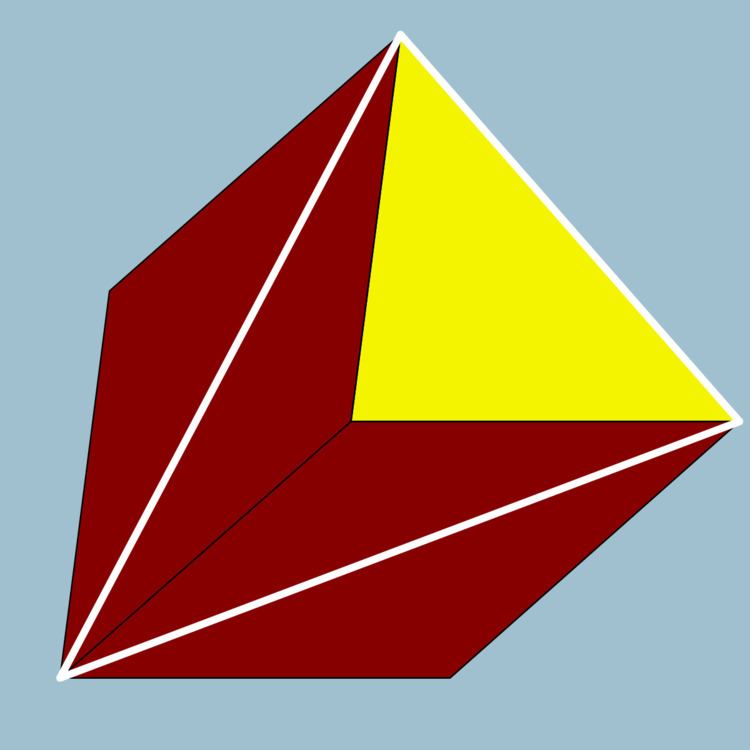
Take some vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure.
More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings, or space-filling tessellation with polytope cells.
As a flat slice
Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This is perhaps the most common approach, and the most easily understood. Different authors make the slice in different places. Wenninger (2003) cuts each edge a unit distance from the vertex, as does Coxeter (1948). For uniform polyhedra the Dorman Luke construction cuts each connected edge at its midpoint. Other authors make the cut through the vertex at the other end of each edge.
For irregular polyhedra, these approaches may produce a vertex figure that does not lie in a plane. A more general approach, valid for arbitrary convex polyhedra, is to make the cut along any plane which separates the given vertex from all the other vertices, but is otherwise arbitrary. This construction determines the combinatorial structure of the vertex figure, similar to a set of connected vertices (see below), but not its precise geometry; it may be generalized to convex polytopes in any dimension.
As a spherical polygon
Cromwell (1999) makes a spherical cut or scoop, centered on the vertex. The cut surface or vertex figure is thus a spherical polygon marked on this sphere.
As the set of connected vertices
Many combinatorial and computational approaches (e.g. Skilling, 1975) treat a vertex figure as the ordered (or partially ordered) set of points of all the neighboring (connected via an edge) vertices to the given vertex.
Abstract definition
In the theory of abstract polytopes, the vertex figure at a given vertex V comprises all the elements which are incident on the vertex; edges, faces, etc. More formally it is the (n−1)-section Fn/V, where Fn is the greatest face.
This set of elements is elsewhere known as a vertex star.
General properties
A vertex figure for an n-polytope is an (n−1)-polytope. For example, a vertex figure for a polyhedron is a polygon figure, and the vertex figure for a 4-polytope is a polyhedron.
By considering the connectivity of these neighboring vertices an (n−1)-polytope, the vertex figure, can be constructed for each vertex of a polytope:
Vertex figures are the most useful for uniform polytopes because one vertex figure can encode the entire polytope.
For polyhedra, the vertex figure can be represented by a vertex configuration notation, by listing the faces in sequence around a vertex. For example 3.4.4.4 is a vertex with one triangle and three squares, and it represents the rhombicuboctahedron.
If the polytope is vertex-transitive, the vertex figure will exist in a hyperplane surface of the n-space. In general the vertex figure need not be planar.
For nonconvex polyhedra, the vertex figure may also be nonconvex. Uniform polytopes, for instance, can have star polygons for faces or for vertex figures.
Dorman Luke construction
For a uniform polyhedron, the face of the dual polyhedron may be found from the original polyhedron's vertex figure using the "Dorman Luke" construction.
Regular polytopes
If a polytope is regular, it can be represented by a Schläfli symbol and both the cell and the vertex figure can be trivially extracted from this notation.
In general a regular polytope with Schläfli symbol {a,b,c,...,y,z} has cells as {a,b,c,...,y}, and vertex figures as {b,c,...,y,z}.
- For a regular polyhedron {p,q}, the vertex figure is {q}, a q-gon.
- Example, the vertex figure for a cube {4,3}, is the triangle {3}.
- For a regular 4-polytope or space-filling tessellation {p,q,r}, the vertex figure is {q,r}.
- Example, the vertex figure for a hypercube {4,3,3}, the vertex figure is a regular tetrahedron {3,3}.
- Also the vertex figure for a cubic honeycomb {4,3,4}, the vertex figure is a regular octahedron {3,4}.
Since the dual polytope of a regular polytope is also regular and represented by the Schläfli symbol indices reversed, it is easy to see the dual of the vertex figure is the cell of the dual polytope. For regular polyhedra, this is a special case of the Dorman Luke construction.
An example vertex figure of a honeycomb
The vertex figure of a truncated cubic honeycomb is a nonuniform square pyramid. One octahedron and four truncated cubes meet at each vertex form a space-filling tessellation.
Edge figure
Related to the vertex figure, an edge figure is the vertex figure of a vertex figure. Edge figures are useful for expressing relations between the elements within regular and uniform polytopes.
An edge figure will be a (n−2)-polytope, representing the arrangement of facets around a given edge. Regular and single-ringed coxeter diagram uniform polytopes will have a single edge type. In general, a uniform polytope can have as many edge types as active mirrors in the construction, since each active mirror produces one edge in the fundamental domain.
Regular polytopes (and honeycombs) have a single edge figure which is also regular. For a regular polytope {p,q,r,s,...,z}, the edge figure is {r,s,...,z}.
In four dimensions, the edge figure of a 4-polytope or 3-honeycomb is a polygon representing the arrangement of a set of facets around an edge. For example, the edge figure for a regular cubic honeycomb {4,3,4} is a square, and for a regular 4-polytope {p,q,r} is the polygon {r}.
Less trivially, the truncated cubic honeycomb t0,1{4,3,4}, has a square pyramid vertex figure, with truncated cube and octahedron cells. Here there are two types of edge figures. One is a square edge figure at the apex of the pyramid. This represents the four truncated cubes around an edge. The other four edge figures are isosceles triangles on the base vertices of the pyramid. These represent the arrangement of two truncated cubes and one octahedron around the other edges.
