Vertices 24 Automorphisms 48 | Edges 36 Chromatic number 3 | |
 | ||
Properties | ||
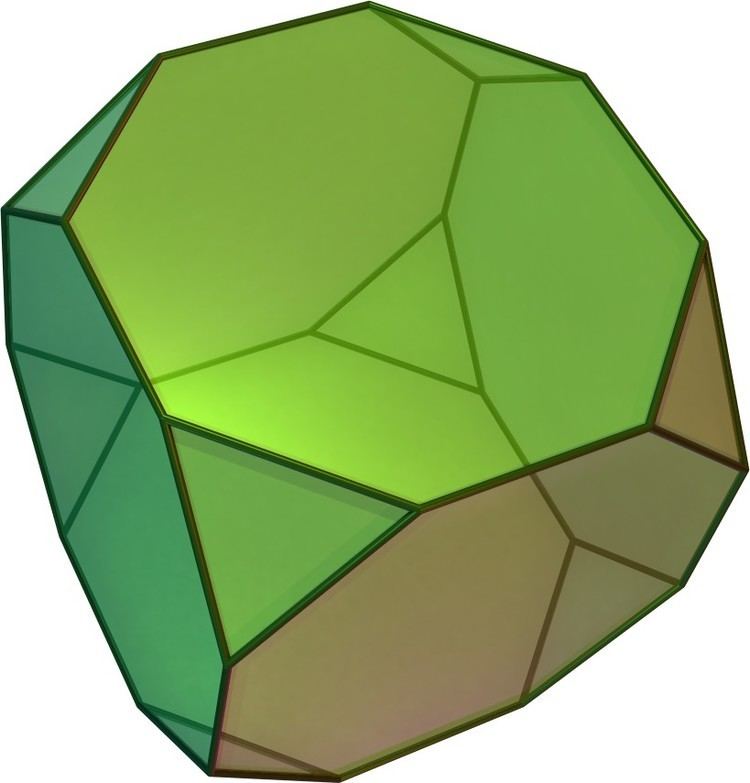
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces (6 octagonal and 8 triangular), 36 edges, and 24 vertices.
Contents
- Area and volume
- Orthogonal projections
- Spherical tiling
- Cartesian coordinates
- Dissection
- Vertex arrangement
- Related polyhedra
- Symmetry mutations
- Alternated truncation
- Related polytopes
- Truncated cubical graph
- References
If the truncated cube has unit edge length, its dual triakis octahedron has edges of lengths 2 and 2 + √2.
Area and volume
The area A and the volume V of a truncated cube of edge length a are:
Orthogonal projections
The truncated cube has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: triangles, and octagons. The last two correspond to the B2 and A2 Coxeter planes.
Spherical tiling
The truncated cube can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
Cartesian coordinates
The following Cartesian coordinates define the vertices of a truncated hexahedron centered at the origin with edge length 2ξ:
(±ξ, ±1, ±1),(±1, ±ξ, ±1),(±1, ±1, ±ξ)where ξ = √2 − 1.
The parameter ξ can be varied between ±1. A value of 1 produces a cube, 0 produces a cuboctahedron, and negative values produces self-intersecting octagrammic faces.
If the self-intersected portions of the octagrams are removed, leaving squares, and truncating the triangles into hexagons, truncated octahedrons are produced, and the sequence ends with the central squares being reduced to a point, and creating an octahedron.
Dissection
The truncated cube can be dissected into a central cube, with six square cupola around each of the cube's faces, and 8 regular tetrahedral in the corners. This dissection can also be seen within the runcic cubic honeycomb, with cube, tetrahedron, and rhombicuboctahedron cells.
This dissection can be used to create a Stewart toroid with all regular faces by removing two square cupola and the central cube. This excavated cube has 16 triangles, 12 squares, and 4 octagons.
Vertex arrangement
It shares the vertex arrangement with three nonconvex uniform polyhedra:
Related polyhedra
The truncated cube is related to other polyhedra and tlings in symmetry.
The truncated cube is one of a family of uniform polyhedra related to the cube and regular octahedron.
Symmetry mutations
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry, and a series of polyhedra and tilings n.8.8.
Alternated truncation
A cube can be alternately truncated producing tetrahedral symmetry, with six hexagonal faces, and four triangles at the truncated vertices. It is one of a sequence of alternate truncations of polyhedra and tiling.
Related polytopes
The truncated cube, is second in a sequence of truncated hypercubes:
Truncated cubical graph
In the mathematical field of graph theory, a truncated cubical graph is the graph of vertices and edges of the truncated cube, one of the Archimedean solids. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.
