Neha Patil (Editor)

Triangle wave

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Triangle wave

A triangle wave is a non-sinusoidal waveform named for its triangular shape. It is a periodic, piecewise linear, continuous real function.

Contents

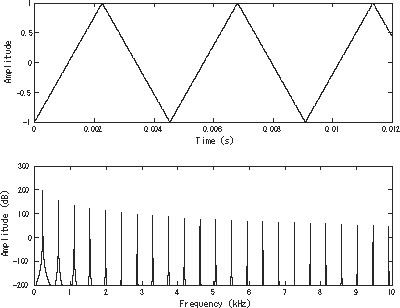
Like a square wave, the triangle wave contains only odd harmonics, demonstrating odd symmetry. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse).

Harmonics

It is possible to approximate a triangle wave with additive synthesis by adding odd harmonics of the fundamental, multiplying every (4n−1)th harmonic by −1 (or changing its phase by π), and rolling off the harmonics by the inverse square of their relative frequency to the fundamental.

This infinite Fourier series converges to the triangle wave with cycle frequency f over time t:

x t r i a n g l e ( t ) = 8 π 2 ∑ k = 0 ∞ ( − 1 ) k sin ⁡ ( 2 π ( 2 k + 1 ) f t ) ( 2 k + 1 ) 2 = 8 π 2 ( sin ⁡ ( 2 π f t ) − 1 9 sin ⁡ ( 6 π f t ) + 1 25 sin ⁡ ( 10 π f t ) − ⋯ )

Definitions

Another definition of the triangle wave, with range from -1 to 1 and period 2a is:

x ( t ) = 2 a ( t − a ⌊ t a + 1 2 ⌋ ) ( − 1 ) ⌊ t a + 1 2 ⌋ where the symbol ⌊ n ⌋ represent the floor function of n.

Also, the triangle wave can be the absolute value of the sawtooth wave:

x ( t ) = | 2 ( t a − ⌊ t a + 1 2 ⌋ ) |

or, for a range from -1 to +1:

x ( t ) = 2 | 2 ( t a − ⌊ t a + 1 2 ⌋ ) | − 1

The triangle wave can also be expressed as the integral of the square wave:

∫ sgn ⁡ ( sin ⁡ ( x ) ) d x

A simple equation with a period of 4, with y ( 0 ) = 1 . As this only uses the modulo operation and absolute value, this can be used to simply implement a triangle wave on hardware electronics with less CPU power:

y ( x ) = | x mod 4 − 2 | − 1

or, a more complex and complete version of the above equation with a period of p , amplitude a , and starting with y ( 0 ) = a / 2 :

y ( x ) = 2 a p ( | ( x mod p ) − p 2 | − p 4 )

The function (1) is a specialization of (2), with a=2 and p=4:

y ( x ) = 2 × 2 4 ( | ( x mod 4 ) − 4 2 | − 4 4 ) ⇔ y ( x ) = ( | ( x mod 4 ) − 2 | − 1 )


An odd version of the function (1) can be made, just shifting by one the input value, which will change the phase of the original function:

y ( x ) = | ( x − 1 ) mod 4 − 2 | − 1

Generalizing the formula (3) to make the function odd for any period and amplitude gives:

y ( x ) = 4 a p ( | ( ( x − p 4 ) mod p ) − p 2 | − p 4 )

In terms of sine and arcsine with period p and amplitude a:

y ( x ) = 2 a π arcsin ⁡ ( sin ⁡ ( 2 π p x ) )

Note: sin y = cos x

Arc Length

The arc length per period "s" for a triangle wave, given the amplitude "a" and period length "p":

s = ( 4 a ) 2 + p 2

References

Triangle wave Wikipedia
(Text) CC BY-SA