Puneet Varma (Editor)

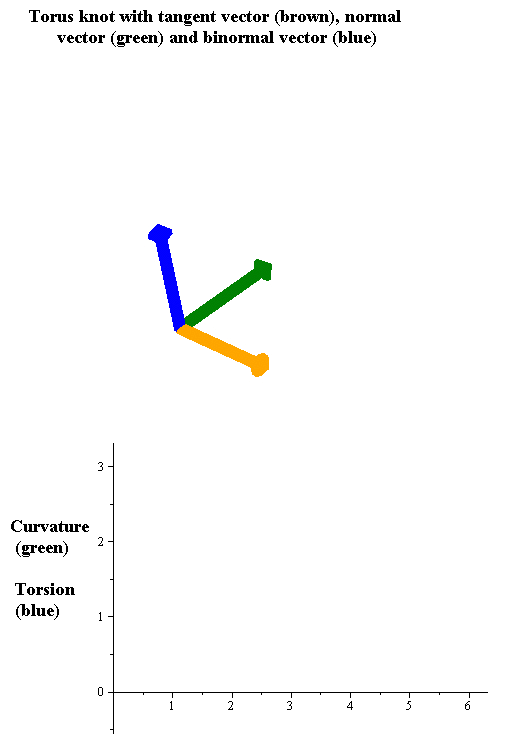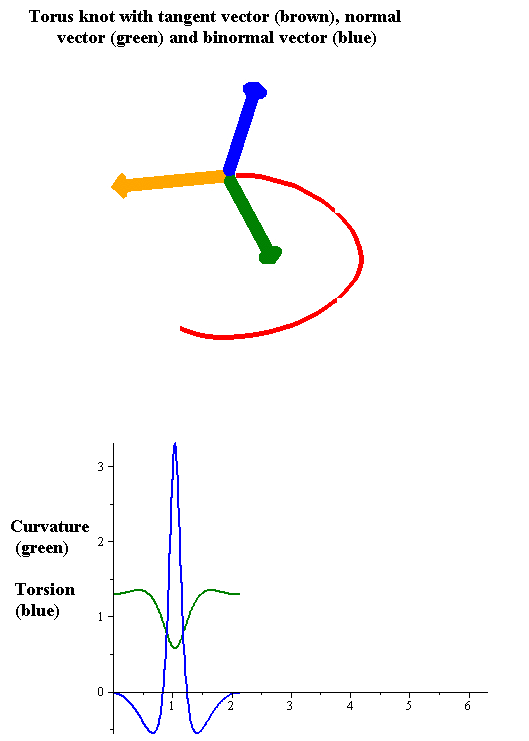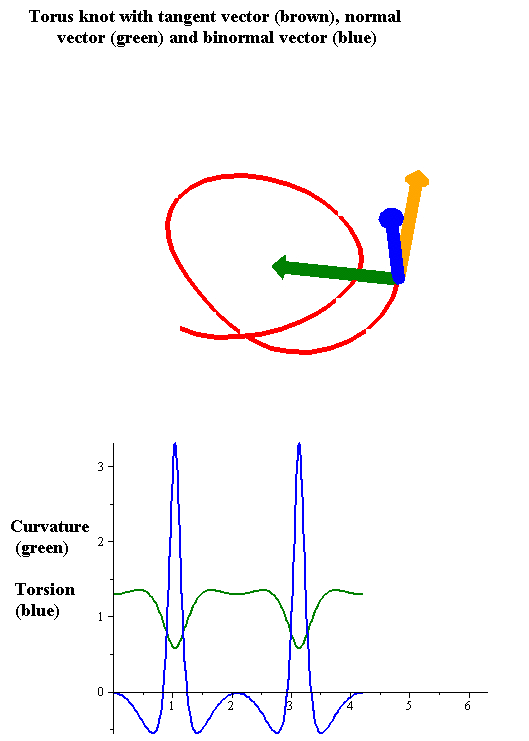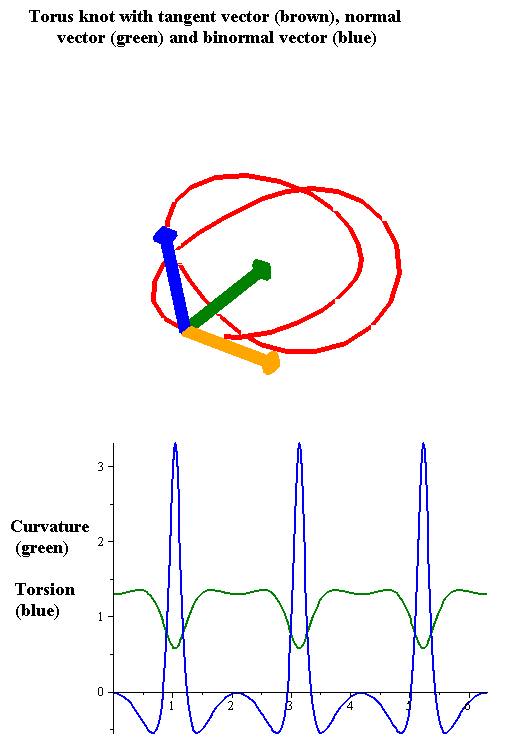
Torsion of a curve

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Torsion of a curve

In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the plane of curvature. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas.

Contents

Definition

Let C be a space curve parametrized by arc length s and with the unit tangent vector t. If the curvature κ of C at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors

n = t ′ κ , b = t × n ,

where the prime denotes the derivative of the vector with respect to the parameter s . The torsion τ measures the speed of rotation of the binormal vector at the given point. It is found from the equation

b ′ = − τ n .

which means

τ = − n ⋅ b ′ .

Remark: The derivative of the binormal vector is perpendicular to both the binormal and the tangent, hence it has to be proportional to the principal normal vector. The negative sign is simply a matter of convention: it is a by-product of the historical development of the subject.

The radius of torsion, often denoted by σ, is defined as

σ = 1 τ .

Geometric relevance: The torsion τ ( s ) measures the turnaround of the binormal vector. The larger the torsion is, the faster the binormal vector rotates around the axis given by the tangent vector (see graphical illustrations). In the animated figure the rotation of the binormal vector is clearly visible at the peaks of the torsion function.

Properties

  • A plane curve with non-vanishing curvature has zero torsion at all points. Conversely, if the torsion of a regular curve with non-vanishing curvature is identically zero, then this curve belongs to a fixed plane.
  • The curvature and the torsion of a helix are constant. Conversely, any space curve whose curvature and torsion are both constant and non-zero is a helix. The torsion is positive for a right-handed helix and is negative for a left-handed one.

    • Alternative description

    Let r = r(t) be the parametric equation of a space curve. Assume that this is a regular parametrization and that the curvature of the curve does not vanish. Analytically, r(t) is a three times differentiable function of t with values in R3 and the vectors

    r ′ ( t ) , r ″ ( t )

    are linearly independent.

    Then the torsion can be computed from the following formula:

    τ = det ( r ′ , r ″ , r ‴ ) ∥ r ′ × r ″ ∥ 2 = ( r ′ × r ″ ) ⋅ r ‴ ∥ r ′ × r ″ ∥ 2 .

    Here the primes denote the derivatives with respect to t and the cross denotes the cross product. For r = (x, y, z), the formula in components is

    τ = x ‴ ( y ′ z ″ − y ″ z ′ ) + y ‴ ( x ″ z ′ − x ′ z ″ ) + z ‴ ( x ′ y ″ − x ″ y ′ ) ( y ′ z ″ − y ″ z ′ ) 2 + ( x ″ z ′ − x ′ z ″ ) 2 + ( x ′ y ″ − x ″ y ′ ) 2 .

    References

    Torsion of a curve Wikipedia
    (Text) CC BY-SA


    Similar Topics