Common objects with this shape Fusilli, Slinky | ||
 | ||
Maya tutorial how to model a cone shaped helix
A helix (pl: helixes or helices) is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helices are coil springs and the handrails of spiral staircases. A "filled-in" helix – for example, a spiral ramp – is called a helicoid. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word helix comes from the Greek word ἕλιξ, "twisted, curved".
Contents
- Maya tutorial how to model a cone shaped helix
- Elsword getting shape in helix step
- Types
- Mathematical description
- Arc length curvature and torsion
- Examples
- References
Elsword getting shape in helix step
Types

Helices can be either right-handed or left-handed. With the line of sight along the helix's axis, if a clockwise screwing motion moves the helix away from the observer, then it is called a right-handed helix; if towards the observer, then it is a left-handed helix. Handedness (or chirality) is a property of the helix, not of the perspective: a right-handed helix cannot be turned to look like a left-handed one unless it is viewed in a mirror, and vice versa.

Most hardware screw threads are right-handed helices. The alpha helix in biology as well as the A and B forms of DNA are also right-handed helices. The Z form of DNA is left-handed.
The pitch of a helix is the height of one complete helix turn, measured parallel to the axis of the helix.
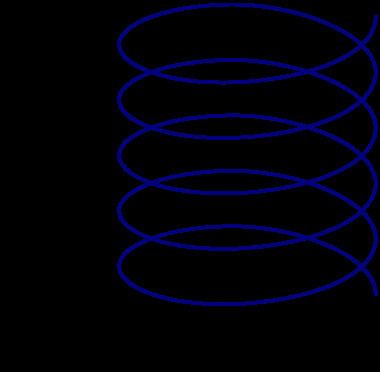
A double helix consists of two (typically congruent) helices with the same axis, differing by a translation along the axis.
A conic helix may be defined as a spiral on a conic surface, with the distance to the apex an exponential function of the angle indicating direction from the axis. An example is the Corkscrew roller coaster at Cedar Point amusement park.
A circular helix, (i.e. one with constant radius) has constant band curvature and constant torsion.
A curve is called a general helix or cylindrical helix if its tangent makes a constant angle with a fixed line in space. A curve is a general helix if and only if the ratio of curvature to torsion is constant.
A curve is called a slant helix if its principal normal makes a constant angle with a fixed line in space. It can be constructed by applying a transformation to the moving frame of a general helix.
Some curves found in nature consist of multiple helices of different handedness joined together by transitions known as tendril perversions.
Mathematical description
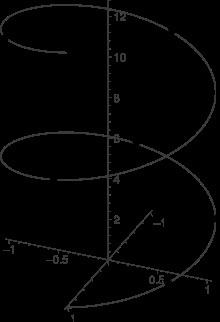
In mathematics, a helix is a curve in 3-dimensional space. The following parametrisation in Cartesian coordinates defines a particular helix, Probably the simplest equations for one is
As the parameter t increases, the point (x(t),y(t),z(t)) traces a right-handed helix of pitch 2θ (or slope 1) and radius 1 about the z-axis, in a right-handed coordinate system.
In cylindrical coordinates (r, θ, h), the same helix is parametrised by:
A circular helix of radius a and slope b/a (or pitch 2θ b) is described by the following parametrisation:
Another way of mathematically constructing a helix is to plot the complex-valued function exi as a function of the real number x (see Euler's formula). The value of x and the real and imaginary parts of the function value give this plot three real dimensions.
Except for rotations, translations, and changes of scale, all right-handed helices are equivalent to the helix defined above. The equivalent left-handed helix can be constructed in a number of ways, the simplest being to negate any one of the x, y or z components.
Arc length, curvature and torsion
The length of a circular helix of radius a and slope b/a (or pitch 2θ b) expressed in rectangular coordinates as
equals
Examples
In music, pitch space is often modeled with helices or double helices, most often extending out of a circle such as the circle of fifths, so as to represent octave equivalency.
