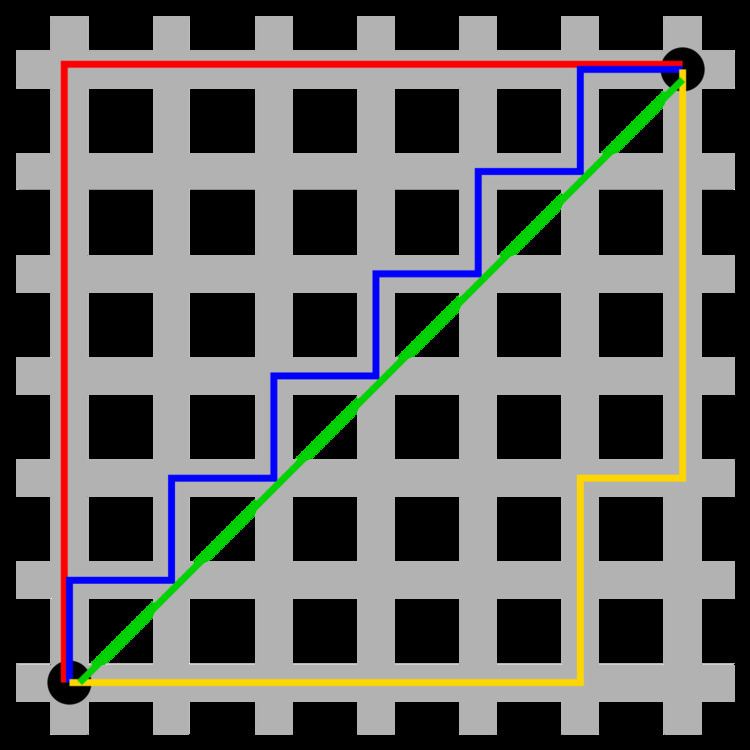
Taxicab geometry - Alchetron, The Free Social Encyclopedia

Taxicab geometry, considered by Hermann Minkowski in 19th-century Germany, is a form of geometry in which the usual distance function of metric or Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their Cartesian coordinates.

The taxicab metric is also known as rectilinear distance, L₁ distance or ℓ 1 norm (see L^p space), snake distance, city block distance, Manhattan distance or Manhattan length, with corresponding variations in the name of the geometry. The latter names allude to the grid layout of most streets on the island of Manhattan, which causes the shortest path a car could take between two intersections in the borough to have length equal to the intersections' distance in taxicab geometry.

Formal definition

The taxicab distance, d 1 , between two vectors p , q in an n-dimensional real vector space with fixed Cartesian coordinate system, is the sum of the lengths of the projections of the line segment between the points onto the coordinate axes. More formally,

d 1 ( p , q ) = ∥ p − q ∥ 1 = ∑ i = 1 n | p i − q i | ,

where ( p , q ) are vectors

p = ( p 1 , p 2 , … , p n ) and q = ( q 1 , q 2 , … , q n )

For example, in the plane, the taxicab distance between ( p 1 , p 2 ) and ( q 1 , q 2 ) is | p 1 − q 1 | + | p 2 − q 2 | .

Properties

Taxicab distance depends on the rotation of the coordinate system, but does not depend on its reflection about a coordinate axis or its translation. Taxicab geometry satisfies all of Hilbert's axioms (a formalization of Euclidean geometry) except for the side-angle-side axiom, as two triangles with equally "long" two sides and an identical angle between them are typically not congruent unless the mentioned sides happen to be parallel.

Circles

A circle is a set of points with a fixed distance, called the radius, from a point called the center. In taxicab geometry, distance is determined by a different metric than in Euclidean geometry, and the shape of circles changes as well. Taxicab circles are squares with sides oriented at a 45° angle to the coordinate axes. The image to the right shows why this is true, by showing in red the set of all points with a fixed distance from a center, shown in blue. As the size of the city blocks diminishes, the points become more numerous and become a rotated square in a continuous taxicab geometry. While each side would have length √2r using a Euclidean metric, where r is the circle's radius, its length in taxicab geometry is 2r. Thus, a circle's circumference is 8r. Thus, the value of a geometric analog to π is 4 in this geometry. The formula for the unit circle in taxicab geometry is | x | + | y | = 1 in Cartesian coordinates and

r = 1 | sin ⁡ θ | + | cos ⁡ θ |

in polar coordinates.

A circle of radius 1 (using this distance) is the von Neumann neighborhood of its center.

A circle of radius r for the Chebyshev distance (L_∞ metric) on a plane is also a square with side length 2r parallel to the coordinate axes, so planar Chebyshev distance can be viewed as equivalent by rotation and scaling to planar taxicab distance. However, this equivalence between L₁ and L_∞ metrics does not generalize to higher dimensions.

Whenever each pair in a collection of these circles has a nonempty intersection, there exists an intersection point for the whole collection; therefore, the Manhattan distance forms an injective metric space.

Measures of distances in chess

In chess, the distance between squares on the chessboard for rooks is measured in taxicab distance; kings and queens use Chebyshev distance, and bishops use the taxicab distance (between squares of the same color) on the chessboard rotated 45 degrees, i.e., with its diagonals as coordinate axes. To reach from one square to another, only kings require the number of moves equal to the distance; rooks, queens and bishops require one or two moves (on an empty board, and assuming that the move is possible at all in the bishop's case).

Compressed sensing

In solving an underdetermined system of linear equations, the regularisation term for the parameter vector is expressed in terms of the ℓ 1 -norm (taxicab geometry) of the vector. This approach appears in the signal recovery framework called compressed sensing.

Differences of frequency distributions

Taxicab geometry can be used to assess the differences in discrete frequency distributions. For example, in RNA splicing positional distributions of hexamers, which plot the probability of each hexamer appearing at each given nucleotide near a splice site, can be compared with L1-distance. Each position distribution can be represented as a vector where each entry represents the likelihood of the hexamer starting at a certain nucleotide. A large L1-distance between the two vectors indicates a significant difference in the nature of the distributions while a small distance denotes similarly shaped distributions. This is equivalent to measuring the area between the two distribution curves because the area of each segment is the absolute difference between the two curves' likelihoods at that point. When summed together for all segments, it provides the same measure as L1-distance.

References

Taxicab geometry Wikipedia

(Text) CC BY-SA

Contents