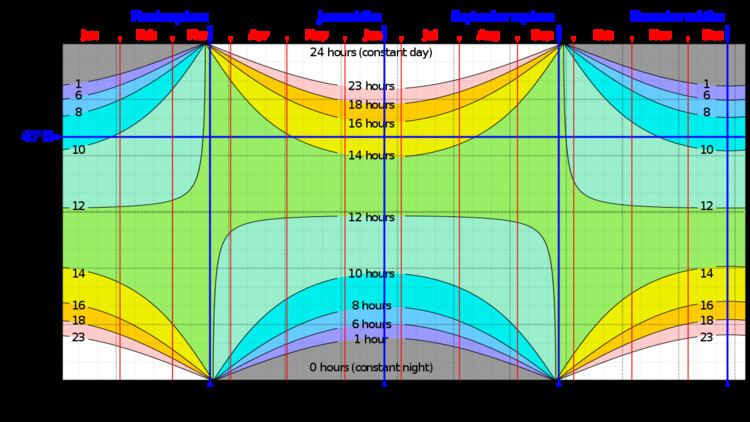
 | ||
The sunrise equation as follows can be used to derive the time of sunrise and sunset for any solar declination and latitude in terms of local solar time when sunrise and sunset actually occur:
Contents
- Theory of the equation
- Generalized equation
- Complete calculation on Earth
- Calculate current Julian day
- Mean solar noon
- Solar mean anomaly
- Equation of the center
- Ecliptic longitude
- Solar transit
- Declination of the Sun
- Hour angle
- Calculate sunrise and sunset
- References
where:
Theory of the equation
The Earth rotates at an angular velocity of 15°/hour. Therefore, the expression
The sign convention is typically that the observer latitude
The expression above is always applicable for latitudes between the Arctic Circle and Antarctic Circle. North of the Arctic Circle or south of the Antarctic Circle, there is at least one day of the year with no sunrise or sunset. Formally, there is a sunrise or sunset when
Generalized equation
Also note that the above equation neglects the influence of atmospheric refraction (which lifts the solar disc by approximately 0.6° when it is on the horizon) and the non-zero angle subtended by the solar disc (about 0.5°). The times of the rising and the setting of the upper solar limb as given in astronomical almanacs correct for this by using the more general equation
with the altitude (a) of the center of the solar disc set to about −0.83° (or −50 arcminutes).
Complete calculation on Earth
The generalized equation relies on a number of other variables which need to be calculated before it can itself be calculated. These equations have the solar-earth constants substituted with angular constants expressed in degrees.
Calculate current Julian day
where:
Mean solar noon
where:
Solar mean anomaly
where:
M is the solar mean anomaly used in a few of next equations.Equation of the center
where:
C is the Equation of the center value needed to calculate lambda (see next equation).Ecliptic longitude
where:
λ is the ecliptic longitude.102.9372 is a value for the argument of perihelion.(Amateur edit, so check before adopting). The value for the "Argument of Perihelion" is not constant, and changes (very slightly) per day. The JPL website gives the following for calculating the true value (valid to 3,000 AD): w0 = 102.9300589 degrees at J2000.0 and wt = 0.3179526 degrees per century (the amount by which this starting value changes). Therefore, one needs to calculate the number of centuries since J2000.0 for the date in question and multiply wt by that value to get the true Argument of Perihelion for the Earth. On 31-Jan-2017 at around 11.0 a.m. London, the elapse time since J2000.0 in centuries el = 6240.0007892/36525 = 0.17084191, so w = w0 + wt * el = 102.984378. The difference is very small, but may make an error in sun rise or set of about a minute as of the example date. Note JPL use 36525 as the number of days in a century, not 36524.22. It seems to work OK.
Solar transit
where:
Jtransit is the Julian date for the local true solar transit (or solar noon).2451545.5 is midnight or the beginning of the equivalent Julian year reference.Declination of the Sun
where:
Hour angle
This is the equation from above with corrections for astronomical refraction and solar disc diameter.
where:
ωo is the hour angle from the observer's zenith;For observations on a sea horizon an elevation-of-observer correction, add
Calculate sunrise and sunset
where:
Jset is the actual Julian date of sunset;Jrise is the actual Julian date of sunrise.