 | ||
In physics, the angular velocity is defined as the rate of change of angular displacement and is a vector quantity (more precisely, a pseudovector) that specifies the angular speed (rotational speed) of an object and the axis about which the object is rotating. This speed can be measured in the SI unit of angular velocity, radians per second, or in terms of degrees per second, degrees per hour, etc. Angular velocity is usually represented by the symbol omega (ω, rarely Ω).
Contents
- Particle in two dimensions
- Particle in three dimensions
- Addition of angular velocity vectors
- Angular velocity vector for a frame
- Components from the vectors of the frame
- Components from Euler angles
- Angular velocity tensor
- Calculation from the orientation matrix
- Properties of angular velocity tensors
- Duality with respect to the velocity vector
- Exponential of W
- W is skew symmetric
- Coordinate free description
- Angular velocity as a vector field
- Rigid body considerations
- Consistency
- References
The direction of the angular velocity vector is perpendicular to the plane of rotation, in a direction that is usually specified by the right-hand rule.
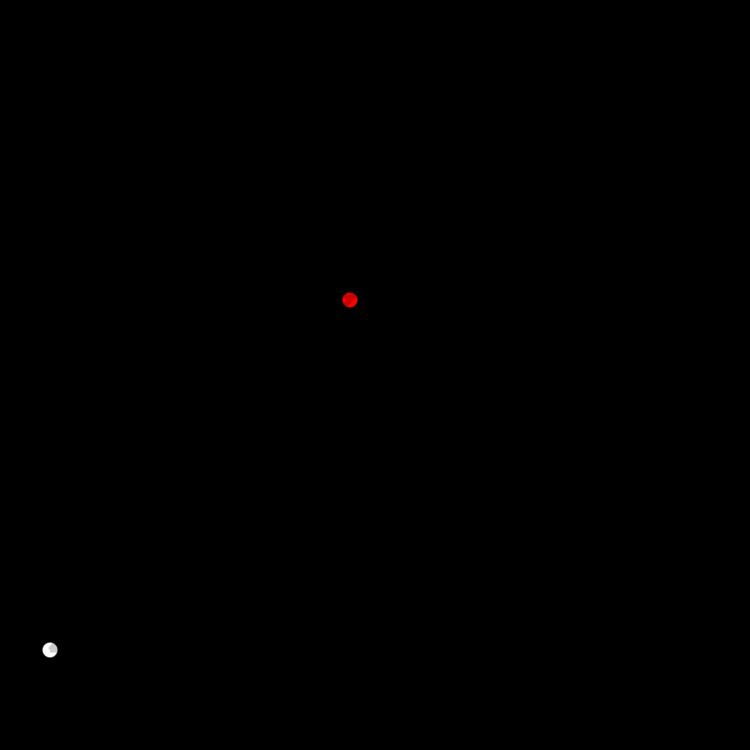
Particle in two dimensions
The angular velocity of a particle is measured around or relative to a point, called the origin. As shown in the diagram (with angles ɸ and θ in radians), if a line is drawn from the origin (O) to the particle (P), then the velocity (v) of the particle has a component along the radius (radial component, v‖) and a component perpendicular to the radius (cross-radial component, v⊥). If there is no radial component, then the particle moves in a circle. On the other hand, if there is no cross-radial component, then the particle moves along a straight line from the origin.
A radial motion produces no change in the direction of the particle relative to the origin, so, for the purpose of finding the angular velocity, the radial component can be ignored. Therefore, the rotation is completely produced by the perpendicular motion around the origin, and the angular velocity is completely determined by this component.
In two dimensions, the angular velocity ω is given by
This is related to the cross-radial (tangential) velocity by:
An explicit formula for v⊥ in terms of v and θ is:
Combining the above equations gives a formula for ω:
In two dimensions, the angular velocity is a single number with an orientation but no direction. The angular velocity in two dimensions is a pseudoscalar, a quantity that changes its sign under a parity inversion (for example if one of the axes is inverted or if axes are swapped). The positive direction of rotation is taken, by convention, to be in the direction towards the y axis from the x axis. If the parity is inverted, but the orientation of a rotation is not, then the sign of the angular velocity changes.
There are three types of angular velocity involved in the movement on an ellipse corresponding to the three anomalies (true, eccentric and mean).
Particle in three dimensions
In three dimensions, the angular velocity becomes a bit more complicated. The angular velocity in this case is generally thought of as a vector, or more precisely, a pseudovector. It now has not only a magnitude, but a direction as well. The magnitude is the angular speed, and the direction describes the axis of rotation that Euler's rotation theorem guarantees must exist. The right-hand rule indicates the positive direction of the angular velocity pseudovector.
Let
Just as in the two dimensional case, a particle will have a component of its velocity along the radius from the origin to the particle, and another component perpendicular to that radius. The combination of the origin point and the perpendicular component of the velocity defines a plane of rotation in which the behavior of the particle (for that instant) appears just as it does in the two dimensional case. The axis of rotation is then a line normal to this plane, and this axis defines the direction of the angular velocity pseudovector, while the magnitude is the same as the pseudoscalar value found in the 2-dimensional case. Using the unit vector
which, by the definition of the cross product, can be written:
and using this vector, it can be seen that the formula for the tangential speed of a point
Addition of angular velocity vectors
Angular velocity can be defined as angular displacement for unit of time. If a point rotates with
With this operation defined like this, angular velocity, which is a pseudovector, also becomes a real vector because it has two operations:
This is the definition of a vector space. The only property that presents difficulties to prove is the commutativity of the addition. This can be proven from the fact that the velocity tensor W (see below) is skew-symmetric. Therefore,
The composition of rotations is not commutative; but, when the rotations are infinitesimal, the first order approximation of the previous series can be taken and
Angular velocity vector for a frame
Given a rotating frame composed by three unitary vectors, all the three must have the same angular speed in any instant. In such a frame, each vector is a particular case of the previous case (moving particle), in which the module of the vector is constant.
Though it just a particular case of a moving particle, this is a very important one for its relationship with the rigid body study, and special tools have been developed for this case. There are two possible ways to describe the angular velocity of a rotating frame: the angular velocity vector and the angular velocity tensor. Both entities are related and they can be calculated from each other.
In a consistent way with the general definition, the angular velocity of a frame is defined as the angular velocity of each of the three vectors of the frame (it will be the same for any of them). The addition of angular velocity vectors for frames is also defined by movement composition, and can be useful to decompose the movement as in a gimbal. Components of the vector can be calculated as derivatives of the parameters defining the moving frames (Euler angles or rotation matrices). As in the general case, addition is commutative:
It is known by Euler's rotation theorem that, for any rotating frame, there always exists an instantaneous axis of rotation in any instant. In the case of a frame, the angular velocity vector is over the instantaneous axis of rotation. Any transversal section of a plane perpendicular to this axis has to behave as a two dimensional rotation. Thus, the magnitude of the angular velocity vector at a given time t is consistent with the two dimensions case.
Components from the vectors of the frame
Substituting in the expression
any unitary vector e of the frame we obtain
As the columns of the matrix of the frame are the components of its vectors, this allows also the calculation of
Components from Euler angles
The components of the angular velocity pseudovector were first calculated by Leonhard Euler using his Euler angles and an intermediate frame made out of the intermediate frames of the construction:
Euler proved that the projections of the angular velocity pseudovector over these three axes was the derivative of its associated angle (which is equivalent to decomposing the instant rotation in three instantaneous Euler rotations). Therefore:
This basis is not orthonormal and it is difficult to use, but now the velocity vector can be changed to the fixed frame or to the moving frame with just a change of bases. For example, changing to the mobile frame:
where
Angular velocity tensor
A similar way to describe the angular speed for a rotating frame is the angular velocity tensor. It can be introduced from rotation matrices. Any vector
We can introduce here the angular velocity tensor associated to the angular speed
Notice that this is an infinitesimal angular displacement divided by an infinitesimal time. This tensor W(t) will act as if it were a
Calculation from the orientation matrix
Given the orientation matrix A(t) of a frame, defined for all t and derivable, we can obtain its instant angular velocity tensor W as follows. We know that:
As angular speed must be the same for the three vectors of a rotating frame, if we have a matrix A(t) whose columns are the vectors of the frame, we can write for the three vectors as a whole:
And therefore the angular velocity tensor we are looking for is:
Properties of angular velocity tensors
In general, the angular velocity in an n-dimensional space is the time derivative of the angular displacement tensor, which is a second rank skew-symmetric tensor.
This tensor W will have n(n-1)/2 independent components and this number is the dimension of the Lie algebra of the Lie group of rotations of an n-dimensional inner product space.
Duality with respect to the velocity vector
In three dimensions, angular velocity can be represented by a pseudovector because second rank tensors are dual to pseudovectors in three dimensions. Notice that the tensor is a matrix with this structure:
As it is a skew symmetric matrix, it has a Hodge dual vector, which is precisely the previous angular velocity vector
Exponential of W
If we know an initial frame A(0) and we are given a constant angular velocity tensor W, we can obtain A(t) for any given t. As
And if the angular speed is constant, then W is also constant and the equation can be integrated. The result is:
which shows a connection with the Lie group of rotations.
W is skew-symmetric
It is possible to prove that angular velocity tensor are skew symmetric matrices, which means that a
To prove it we start taking the time derivative of
Applying the formula (AB)T = BTAT:
Thus, W is the negative of its transpose, which implies it is a skew symmetric matrix.
Coordinate-free description
At any instant,
where we omitted the
The relation between this linear map and the angular velocity pseudovector
Because of W is the derivative of an orthogonal transformation, the
bilinear form is skew-symmetric. (Here
where
Taking the dual vector L* of L we get
Introducing
where
by definition.
Because
Angular velocity as a vector field
For angular velocity tensor maps velocities to positions, it is a vector field. In particular, this vector field is a Killing vector field belonging to an element of the Lie algebra so(3) of the 3-dimensional rotation group SO(3). This element of so(3) can also be regarded as the angular velocity vector.
Rigid body considerations
The same equations for the angular speed can be obtained reasoning over a rotating rigid body. Here is not assumed that the rigid body rotates around the origin. Instead, it can be supposed rotating around an arbitrary point that is moving with a linear velocity V(t) in each instant.
To obtain the equations, it is convenient to imagine a rigid body attached to the frames and consider a coordinate system that is fixed with respect to the rigid body. Then we will study the coordinate transformations between this coordinate and the fixed "laboratory" system.
As shown in the figure on the right, the lab system's origin is at point O, the rigid body system origin is at O' and the vector from O to O' is R. A particle (i) in the rigid body is located at point P and the vector position of this particle is Ri in the lab frame, and at position ri in the body frame. It is seen that the position of the particle can be written:
The defining characteristic of a rigid body is that the distance between any two points in a rigid body is unchanging in time. This means that the length of the vector
Taking the time derivative yields the velocity of the particle:
where Vi is the velocity of the particle (in the lab frame) and V is the velocity of O' (the origin of the rigid body frame). Since
or
where
It can be proved that this is a skew symmetric matrix, so we can take its dual to get a 3 dimensional pseudovector that is precisely the previous angular velocity vector
Substituting ω for W into the above velocity expression, and replacing matrix multiplication by an equivalent cross product:
It can be seen that the velocity of a point in a rigid body can be divided into two terms – the velocity of a reference point fixed in the rigid body plus the cross product term involving the angular velocity of the particle with respect to the reference point. This angular velocity is the "spin" angular velocity of the rigid body as opposed to the angular velocity of the reference point O' about the origin O.
Consistency
We have supposed that the rigid body rotates around an arbitrary point. We should prove that the angular velocity previously defined is independent from the choice of origin, which means that the angular velocity is an intrinsic property of the spinning rigid body.
See the graph to the right: The origin of lab frame is O, while O1 and O2 are two fixed points on the rigid body, whose velocity is
The above two yields that
Since the point P (and thus
If the reference point is the instantaneous axis of rotation the expression of velocity of a point in the rigid body will have just the angular velocity term. This is because the velocity of instantaneous axis of rotation is zero. An example of instantaneous axis of rotation is the hinge of a door. Another example is the point of contact of a purely rolling spherical (or, more generally, convex) rigid body.
