 | ||
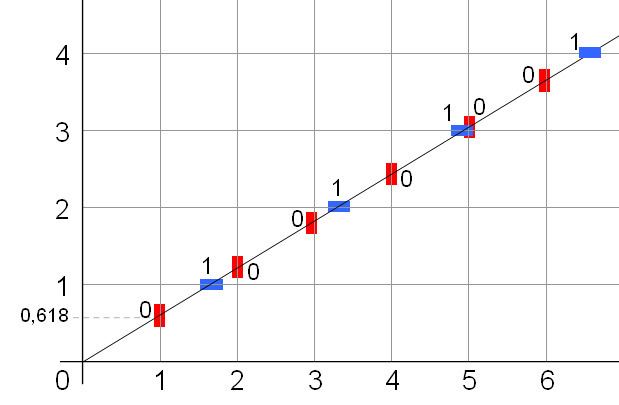
In mathematics, a Sturmian word (Sturmian sequence or billiard sequence), named after Jacques Charles François Sturm, is a certain kind of infinitely long sequence of characters. Such a sequence can be generated by considering a game of English billiards on a square table. The struck ball will successively hit the vertical and horizontal edges labelled 0 and 1 generating a sequence of letters. This sequence is a Sturmian word.
Contents
Definition
Sturmian sequences can be defined strictly in terms of their combinatoric properties or geometrically as cutting sequences for lines of irrational slope or codings for irrational rotations. They are traditionally taken to be infinite sequences on the alphabet of the two symbols 0 and 1.
Sequences of low complexity
For an infinite sequence of symbols w, let σ(n) be the complexity function of w; i.e., σ(n) = the number of distinct subwords in w of length n. w is Sturmian if σ(n)=n+1 for all n.
Balanced sequences
A set X of binary strings is called balanced if the Hamming weight of elements of X takes at most two distinct values. That is, for any
Let w be an infinite sequence of 0s and 1s and let
Cutting sequence of irrational
Let w be an infinite sequence of 0s and 1s. The sequence w is Sturmian if for some
Difference of Beatty sequences
Let w=(wn) be an infinite sequence of 0s and 1s. The sequence w is Sturmian if it is the difference of non-homogeneous Beatty sequences, that is, for some
for all
for all
Coding of irrational rotation
For
Let w be an infinite sequence of 0s and 1s. The sequence w is Sturmian if for some
Example
A famous example of a (standard) Sturmian word is the Fibonacci word; its slope is
Balanced aperiodic sequences
A set S of finite binary words is balanced if for each n the subset Sn of words of length n has the property that the Hamming weight of the words in Sn takes at most two distinct values. A balanced sequence is one for which the set of factors is balanced. A balanced sequence has at most n+1 distinct factors of length n. An aperiodic sequence is one which does not consist of a finite sequence followed by a finite cycle. An aperiodic sequence has at least n+1 distinct factors of length n. A sequence is Sturmian if and only if it is balanced and aperiodic.
Slope and intercept
A sequence
for all
All the Sturmian words corresponding to the same slope
The standard word
Let
where the product between words is just their concatenation. Every word in the sequence
The infinite sequence of words
A Sturmian word w over {0,1} is characteristic if and only if both 0w and 1w are Sturmian.
Frequencies
If s is an infinite sequence word and w is a finite word, let μN(w) denote the number of occurrences of w as a factor in the prefix of s of length N+|w|-1. If μN(w) has a limit as N→∞, we call this the frequency of w, denoted by μ(w).
For a Sturmian word s, every finite factor has a frequency. The three-distance theorem states that the factors of fixed length n have at most three distinct frequencies, and if there are three values then one is the sum of the other two.
Non-binary words
For words over an alphabet of size k greater than 2, we define a Sturmian word to be one with complexity function n+k−1. They can be described in terms of cutting sequences for k-dimensional space. An alternative definition is as words of minimal complexity subject to not being ultimately periodic.
Associated real numbers
A real number for which the digits with respect to some fixed base form a Sturmian word is a transcendental number.
History
Although the study of Sturmian words dates back to Johann III Bernoulli (1772), it was Gustav A. Hedlund and Marston Morse in 1940 who coined the term Sturmian to refer to such sequences, in honor of the mathematician Jacques Charles François Sturm due to the relation with the Sturm comparison theorem.
