Fibonacci word

Definition

Let S 0 be "0" and S 1 be "01". Now S n = S n − 1 S n − 2 (the concatenation of the previous sequence and the one before that).

The infinite Fibonacci word is the limit S ∞ .

Enumerating items from the above definition produces:

S 0    0

S 1    01

S 2    010

S 3    01001

S 4    01001010

S 5    0100101001001

...

The first few elements of the infinite Fibonacci word are:

0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, ... (sequence A003849 in the OEIS)

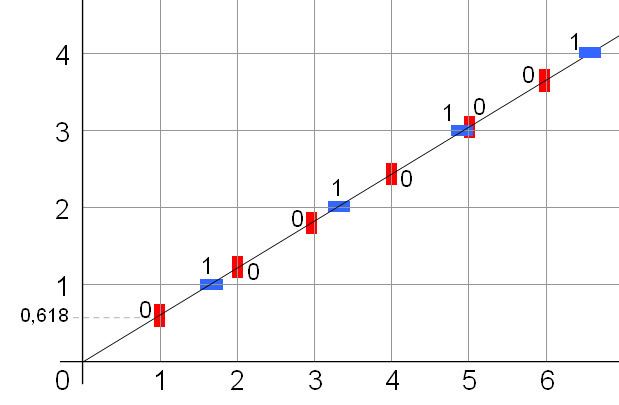
Closed-form expression for individual digits

The n^th digit of the word is 2 + ⌊ n φ ⌋ − ⌊ ( n + 1 ) φ ⌋ where φ is the golden ratio and ⌊ x ⌋ is the floor function (sequence A003849 in the OEIS).

Substitution rules

Another way of going from S_n to S_n + 1 is to replace each symbol 0 in S_n with the pair of consecutive symbols 0, 1 in S_n + 1, and to replace each symbol 1 in S_n with the single symbol 0 in S_n + 1.

Alternatively, one can imagine directly generating the entire infinite Fibonacci word by the following process: start with a cursor pointing to the single digit 0. Then, at each step, if the cursor is pointing to a 0, append 1, 0 to the end of the word, and if the cursor is pointing to a 1, append 0 to the end of the word. In either case, complete the step by moving the cursor one position to the right.

A similar infinite word, sometimes called the rabbit sequence, is generated by a similar infinite process with a different replacement rule: whenever the cursor is pointing to a 0, append 1, and whenever the cursor is pointing to a 1, append 0, 1. The resulting sequence begins

0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, ...

However this sequence differs from the Fibonacci word only trivially, by swapping 0s for 1s and shifting the positions by one.

A closed form expression for the so-called rabbit sequence:

The n^th digit of the word is ⌊ n φ ⌋ − ⌊ ( n − 1 ) φ ⌋ − 1 where φ is the golden ratio and ⌊ x ⌋ is the floor function.

Discussion

The word is related to the famous sequence of the same name (the Fibonacci sequence) in the sense that addition of integers in the inductive definition is replaced with string concatenation. This causes the length of S_n to be F_n + 2, the (n + 2)th Fibonacci number. Also the number of 1s in S_n is F_n and the number of 0s in S_n is F_n + 1.

Other properties

The infinite Fibonacci word is not periodic and not ultimately periodic.

The last two letters of a Fibonacci word are alternately "01" and "10".

Suppressing the last two letters of a Fibonacci word, or prefixing the complement of the last two letters, creates a palindrome. Example: 01 S 4 = 0101001010 is a palindrome. The palindromic density of the infinite Fibonacci word is thus 1/φ, where φ is the Golden ratio: this is the largest possible value for aperiodic words.

In the infinite Fibonacci word, the ratio (number of letters)/(number of zeroes) is φ, as is the ratio of zeroes to ones.

The infinite Fibonacci word is a balanced sequence: Take two factors of the same length anywhere in the Fibonacci word. The difference between their Hamming weights (the number of occurrences of "1") never exceeds 1.

The subwords 11 and 000 never occur.

The complexity function of the infinite Fibonacci word is n+1: it contains n+1 distinct subwords of length n. Example: There are 4 distinct subwords of length 3 : "001", "010", "100" and "101". Being also non-periodic, it is then of "minimal complexity", and hence a Sturmian word, with slope 1 / ϕ 2 . The infinite Fibonacci word is the standard word generated by the directive sequence (1,1,1,....).

The infinite Fibonacci word is recurrent; that is, every subword occurs infinitely often.

If u is a subword of the infinite Fibonacci word, then so is its reversal, denoted u R .

If u is a subword of the infinite Fibonacci word, then the least period of u is a Fibonacci number.

The concatenation of two successive Fibonacci words is "almost commutative". S n + 1 = S n S n − 1 and S n − 1 S n differ only by their last two letters.

As a consequence, the infinite Fibonacci word can be characterized by a cutting sequence of a line of slope ϕ or ϕ − 1 . See figure above.

The number 0.010010100..., whose decimals are built with the digits of the infinite Fibonacci word, is transcendental.

The letters "1" can be found at the positions given by the successive values of the Upper Wythoff sequence (OEIS A001950): ⌊ n ϕ 2 ⌋

The letters "0" can be found at the positions given by the successive values of the Lower Wythoff sequence (OEIS A000201): ⌊ n ϕ ⌋

The distribution of n = F k points on the unit circle, placed consecutively clockwise by the golden angle 2 π ϕ 2 , generates a pattern of two lengths 2 π ϕ k − 1 , 2 π ϕ k on the unit circle. Although the above generating process of the Fibonacci word does not correspond directly to the successive division of circle segments, this pattern is S k − 1 if the pattern starts at the point nearest to the first point in clockwise direction, whereupon 0 corresponds to the long distance and 1 to the short distance.

The infinite Fibonacci word can contain repetitions of 3 successive identical subwords, but never 4. The critical exponent for the infinite Fibonacci word is 2 + ϕ = 3.618 repetitions. It is the smallest index (or critical exponent) among all Sturmian words.

The infinite Fibonacci word is often cited as the worst case for algorithms detecting repetitions in a string.

The infinite Fibonacci word is a morphic word, generated in {0,1}* by the endomorphism 0 → 01, 1 → 0.

Applications

Fibonacci based constructions are currently used to model physical systems with aperiodic order such as quasicrystals. Crystal growth techniques have been used to grow Fibonacci layered crystals and study their light scattering properties.