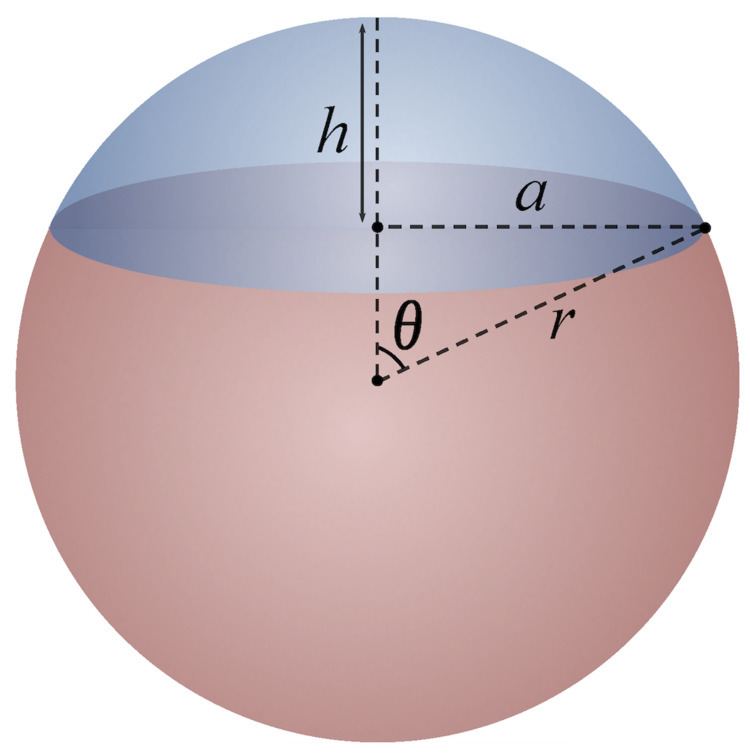
In geometry, a spherical cap, spherical dome, or spherical segment of one base is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.
Volume and surface area
If the radius of the base of the cap is a , and the height of the cap is h , then the volume of the spherical cap is
V = π h 6 ( 3 a 2 + h 2 ) and the curved surface area of the spherical cap is
A = 2 π r h or
A = 2 π r 2 ( 1 − cos θ ) The relationship between h and r is irrelevant as long as 0 ≤ h ≤ 2 r . The red section of the illustration is also a spherical cap.
The parameters a , h and r are not independent:
r 2 = ( r − h ) 2 + a 2 = r 2 + h 2 − 2 r h + a 2 r = a 2 + h 2 2 h Substituting this into the area formula gives:
A = 2 π ( a 2 + h 2 ) 2 h h = π ( a 2 + h 2 ) .
Note also that in the upper hemisphere of the diagram, h = r − r 2 − a 2 , and in the lower hemisphere h = r + r 2 − a 2 ; hence in either hemisphere a = h ( 2 r − h ) and so an alternative expression for the volume is
V = π h 2 3 ( 3 r − h ) .
The volume may also be found by integrating under a surface of rotation, using x = r cos ( θ ) and factorizing.
V = ∫ x r π ( r 2 − x 2 ) d x = π ( 2 3 r 3 − r 2 x + 1 3 x 3 ) = π 3 r 3 ( cos ( θ ) + 2 ) ( cos ( θ ) − 1 ) 2 .
Volumes of union and intersection of two intersecting spheres
The volume of the union of two intersecting spheres of radii r1 and r2 is
V = V ( 1 ) − V ( 2 ) ,
where
V ( 1 ) = 4 π 3 r 1 3 + 4 π 3 r 2 3 is the sum of the volumes of the two isolated spheres, and
V ( 2 ) = π h 1 2 3 ( 3 r 1 − h 1 ) + π h 2 2 3 ( 3 r 2 − h 2 ) the sum of the volumes of the two spherical caps forming their intersection. If d < r1 + r2 is the distance between the two sphere centers, elimination of the variables h1 and h2 leads to
V ( 2 ) = π 12 d ( r 1 + r 2 − d ) 2 ( d 2 + 2 d ( r 1 + r 2 ) − 3 ( r 1 − r 2 ) 2 ) .
The surface area bounded by two circles of latitude is the difference of surface areas of their respective spherical caps. For a sphere of radius r, and latitudes φ1 and φ2, the area is
A = 2 π r 2 | sin ϕ 1 − sin ϕ 2 | For example, assuming the Earth is a sphere of radius 6371 km, the surface area of the arctic (north of the Arctic Circle, at latitude 66.56° as of August 2016) is 2π·6371²|sin 90° − sin 66.56°| = 21.04 million km², or 0.5·|sin 90° − sin 66.56°| = 4.125% of the total surface area of the Earth.
The spheroidal dome is obtained by sectioning off a portion of a spheroid so that the resulting dome is circularly symmetric (having an axis of rotation), and likewise the ellipsoidal dome is derived from the ellipsoid.
Generally, the n -dimensional volume of a hyperspherical cap of height h and radius r in n -dimensional Euclidean space is given by
V = π n − 1 2 r n Γ ( n + 1 2 ) ∫ 0 arccos ( r − h r ) sin n ( t ) d t where Γ (the gamma function) is given by Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t .
The formula for V can be expressed in terms of the volume of the unit n-ball C n = π n / 2 / Γ [ 1 + n 2 ] and the hypergeometric function 2 F 1 or the regularized incomplete beta function I x ( a , b ) as
V = C n r n ( 1 2 − r − h r Γ [ 1 + n 2 ] π Γ [ n + 1 2 ] 2 F 1 ( 1 2 , 1 − n 2 ; 3 2 ; ( r − h r ) 2 ) ) = 1 2 C n r n I ( 2 r h − h 2 ) / r 2 ( n + 1 2 , 1 2 ) ,
and the area formula A can be expressed in terms of the area of the unit n-ball A n = 2 π n / 2 / Γ [ n 2 ] as
A = 1 2 A n r n − 1 I ( 2 r h − h 2 ) / r 2 ( n − 1 2 , 1 2 ) ,
where 0 ≤ h ≤ r .
Earlier in (1986, USSR Academ. Press) the following formulas were derived: A = A n p n − 2 ( q ) , V = C n p n ( q ) , where q = 1 − h / r ( 0 ≤ q ≤ 1 ) , p n ( q ) = ( 1 − G n ( q ) / G n ( 1 ) ) / 2 ,
G n ( q ) = ∫ 0 q ( 1 − t 2 ) ( n − 1 ) / 2 d t .
For odd n = 2 k + 1 :
G n ( q ) = ∑ i = 0 k ( − 1 ) i ( k i ) q 2 i + 1 2 i + 1 .
It is shown in that, if n → ∞ and q n = const. , then p n ( q ) → 1 − F ( q n ) where F ( ) is the integral of the standard normal distribution.
Richmond, Timothy J. (1984). "Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect". J. Mol. Biol. 178 (1): 63–89. doi:10.1016/0022-2836(84)90231-6. Lustig, Rolf (1986). "Geometry of four hard fused spheres in an arbitrary spatial configuration". Mol. Phys. 59 (2): 195–207. Bibcode:1986MolPh..59..195L. doi:10.1080/00268978600102011. Gibson, K. D.; Scheraga, Harold A. (1987). "Volume of the intersection of three spheres of unequal size: a simplified formula". J. Phys. Chem. 91 (15): 4121–4122. doi:10.1021/j100299a035. Gibson, K. D.; Scheraga, Harold A. (1987). "Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii". Mol. Phys. 62 (5): 1247–1265. Bibcode:1987MolPh..62.1247G. doi:10.1080/00268978700102951. Petitjean, Michel (1994). "On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects". Int. J. Quant. Chem. 15 (5): 507–523. doi:10.1002/jcc.540150504. Grant, J. A.; Pickup, B. T. (1995). "A Gaussian description of molecular shape". J. Phys. Chem. 99 (11): 3503–3510. doi:10.1021/j100011a016. Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). "ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations". Comp. Phys. Commun. 165: 59–96. Bibcode:2005CoPhC.165...59B. doi:10.1016/j.cpc.2004.08.002.