Resolvent cubic

Definitions

Suppose that the coefficients of P(x) belong to a field k whose characteristic is different from 2. In other words, we are working in a field in which 1 + 1 ≠ 0. Whenever roots of P(x) are mentioned, they belong to some extension K of k such that P(x) factors into linear factors in K[x]. If k is the field Q of rational numbers, then K can be the field C of complex numbers or the field Q of algebraic numbers.

In some cases, the concept of resolvent cubic is defined only when P(x) is a quartic in depressed form—that is, when a₃ = 0.

Note that the fourth and fifth definitions below also make sense and that the relationship between these resolvent cubics and P(x) are still valid if the characteristic of k is equal to 2.

First definition

Suppose that P(x) is a depressed quartic—that is, that a₃ = 0. A possible definition of the resolvent cubic of P(x) is:

The origin of this definition lies in applying Ferrari's method to find the roots of P(x). To be more precise:

Add a new unknown, y, to x² + a₂/2. Now you have:

If this expression is a square, it can only be the square of

But the equality

is equivalent to

and this is the same thing as the assertion that R₁(y) = 0.

If y₀ is a root of R₁(y), then it is a consequence of the computations made above that the roots of P(x) are the roots of the polynomial

together with the roots of the polynomial

Of course, this makes no sense if y₀ = 0, but since the constant term of R₁(y) is –a₁², 0 is a root of R₁(y) if and only if a₁ = 0, and in this case the roots of P(x) can be found using the quadratic formula.

Second definition

Another possible definition (still supposing that P(x) is a depressed quartic) is

The origin of this definition is similar to the previous one. This time, we start by doing:

and a computation similar to the previous one shows that this last expression is a square if and only if

A simple computation shows that

Third definition

Another possible definition (again, supposing that P(x) is a depressed quartic) is

The origin of this definition lies in another method of solving quartic equations, namely Descartes' method. If you try to find the roots of P(x) by expressing it as a product of two monic quadratic polynomials x² + αx + β and x² – αx + γ, then

If there is a solution of this system with α ≠ 0 (note that if a₁ ≠ 0, then this is automatically true for any solution), the previous system is equivalent to

It is a consequence of the first two equations that then

and

After replacing, in the third equation, β and γ by these values one gets that

and this is equivalent to the assertion that α² is a root of R₃(y). So, again, knowing the roots of R₃(y) helps to determine the roots of P(x).

Note that

Fourth definition

Still another possible definition is

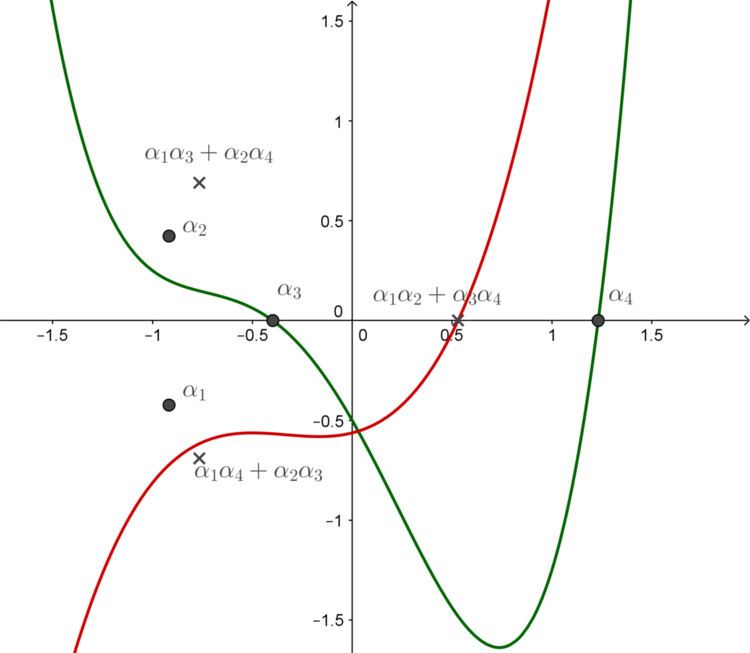
In fact, if the roots of P(x) are α₁, α₂, α₃, and α₄, then

a fact the follows from Vieta's formulas. In other words, R₄(y) is the monic polynomial whose roots are α₁α₂ + α₃α₄, α₁α₃ + α₂α₄, and α₁α₄ + α₂α₃.

It is easy to see that

and

Therefore, P(x) has a multiple root if and only if R₄(y) has a multiple root. More precisely, P(x) and R₄(y) have the same discriminant.

One should note that if P(x) is a depressed polynomial, then

Fifth definition

Yet another definition is

If, as above, the roots of P(x) are α₁, α₂, α₃, and α₄, then

again as a consequence of Vieta's formulas. In other words, R₅(y) is the monic polynomial whose roots are (α₁ + α₂)(α₃ + α₄), (α₁ + α₃)(α₂ + α₄), and (α₁ + α₄)(α₂ + α₃).

It is easy to see that

and

Therefore, as it happens with R₄(y), P(x) has a multiple root if and only if R₅(y) has a multiple root. More precisely, P(x) and R₅(y) have the same discriminant. This is also a consequence of the fact that R₅(y + a₂) = R₄(y).

Note that if P(x) is a depressed polynomial, then

Solving quartic equations

It was explained above how R₁(y), R₂(y), and R₃(y) can be used to find the roots of P(x) if this polynomial is depressed. In the general case, one simply has to find the roots of the depressed polynomial P(x − a₃/4). For each root x₀ of this polynomial, x₀ − a₃/4 is a root of P(x).

Factoring quartic polynomials

If a quartic polynomial P(x) is reducible in k[x], then it is the product of two quadratic polynomials or the product of a linear polynomial by a cubic polynomial. This second possibility occurs if and only if P(x) has a root in k. In order to determine whether or not P(x) can be expressed as the product of two quadratic polynomials, let us assume, for simplicity, that P(x) is a depressed polynomial. Then it was seen above that if the resolvent cubic R₃(y) has a non-null root of the form α², for some α ∈ k, then such a decomposition exists.

This can be used to prove that, in R[x], every quartic polynomial without real roots can be expressed as the product of two quadratic polynomials. Let P(x) be such a polynomial. We can assume without loss of generality that P(x) is monic. We can also assume without loss of generality that it is a reduced polynomial, because P(x) can be expressed as the product of two quadratic polynomials if and only if P(x − a₃/4) can and this polynomial is a reduced one. Then R₃(y) = y³ + 2a₂y² + (a₂² − 4a₀)y − a₁². There are two cases:

More generally, if k is a real closed field, then every quartic polynomial without roots in k can be expressed as the product of two quadratic polynomials in k[x]. Indeed, this statement can be expressed in first-order logic and any such statement that holds for R also holds for any real closed field.

A similar approach can be used to get an algorithm to determine whether or not a quartic polynomial P(x) ∈ Q[x] is reducible and, if it is, how to express it as a product of polynomials of smaller degree. Again, we will suppose that P(x) is monic and depressed. Then P(x) is reducible if and only if at least one of the following conditions holds:

Indeed:

Galois groups of irreducible quartic polynomials

The resolvent cubic of an irreducible quartic polynomial P(x) can be used to determine its Galois group G; that is, the Galois group of the splitting field of P(x). Let m be the degree over k of the splitting field of the resolvent cubic (it can be either R₄(y) or R₅(y); they have the same splitting field). Then the group G is a subgroup of the symmetric group S₄. More precisely: