 | ||
Quantum non-equilibrium is a concept within stochastic formulations of the De Broglie–Bohm theory of quantum physics.
Contents
In the Copenhagen interpretation, that is, the most widely used interpretation of quantum mechanics, the Born rule
This is not the case for the De Broglie–Bohm theory, where the Born rule is not a basic law. Rather, in this theory the link between the probability density and the wave function has the status of a hypothesis, called the quantum equilibrium hypothesis, which is additional to the basic principles governing the wave function, the dynamics of the quantum particles and the Schrödinger equation. (For mathematical details, refer to the derivation by Peter R. Holland.)
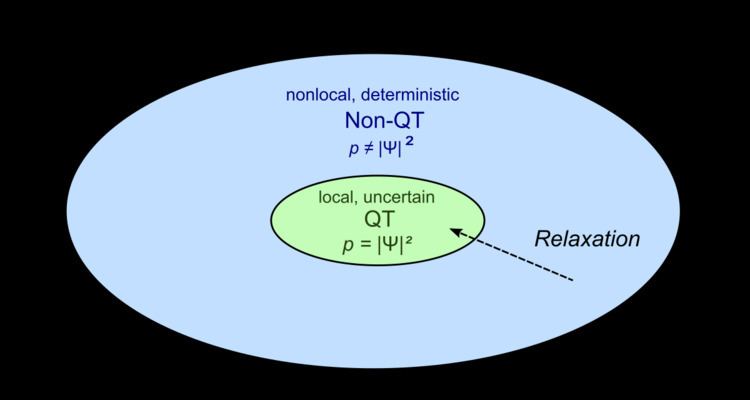
Accordingly, quantum non-equilibrium describes a state of affairs where the Born rule is not fulfilled; that is, the probability to find the particle in the differential volume
Recent advances in investigations into properties of quantum non-equilibrium states have been performed mainly by theoretical physicist Antony Valentini, and earlier steps in this direction were undertaken by David Bohm, Jean-Pierre Vigier, Basil Hiley and Peter R. Holland. The existence of quantum non-equilibrium states has not been verified experimentally; quantum non-equilibrium is so far a theoretical construct. The relevance of quantum non-equilibrium states to physics lies in the fact that they can lead to different predictions for results of experiments, depending on whether the De Broglie–Bohm theory in its stochastic form or the Copenhagen interpretation is assumed to describe reality. (The Copenhagen interpretation, which stipulates the Born rule a priori, does not foresee the existence of quantum non-equilibrium states at all.) That is, properties of quantum non-equilibrium can make certain classes of Bohmian theories falsifiable according to the criterion of Karl Popper.
In practice, when performing Bohmian mechanics computations in quantum chemistry, the quantum equilibrium hypothesis is simply considered to be fulfilled, in order to predict system behaviour and the outcome of measurements.
Relaxation to equilibrium
The causal interpretation of quantum mechanics has been set up by de Broglie and Bohm as a causal, deterministic model, and it was extended later by Bohm, Vigier, Hiley, Valentini and others to include stochastic properties.
Bohm and other physicists, including Valentini, view the Born rule linking
In 1991, Valentini provided indications for deriving the quantum equilibrium hypothesis which states that
Valentini's derivation of the quantum equilibrium hypothesis was criticized by Detlef Dürr and co-workers in 1992, and the derivation of the quantum equilibrium hypothesis has remained a topic of active investigation.
Numerical simulations demonstrate a tendency for Born rule distributions to arise spontaneously at short time scales.
Predicted properties of quantum non-equilibrium
Valentini showed that his expansion of the De Broglie–Bohm theory would allow “signal nonlocality” for non-equilibrium cases in which
Valentini furthermore showed that an ensemble of particles with known wave function and known nonequilibrium distribution could be used to perform, on another system, measurements that violate the uncertainty principle.
These predictions differ from predictions that would result from approaching the same physical situation by means of the Copenhagen interpretation and therefore would in principle make the predictions of this theory accessible to experimental study. As it is unknown whether or how quantum non-equilibrium states can be produced, it is difficult or impossible to perform such experiments.
However, also the hypothesis of quantum non-equilibrium big bang gives rise to quantitative predictions for nonequilibrium deviations from quantum theory which appear to be more easily accessible to observation.
