 | ||
Quadray coordinates, also known as tetray coordinates or Chakovian coordinates, were Invented by Darrel Jarmusch and further developed by David Chako, Tom Ace, Kirby Urner, et al., as another take on simplicial coordinates, a coordinate system using a simplex or tetrahedron as its basis polyhedron.
Contents
Geometric definition
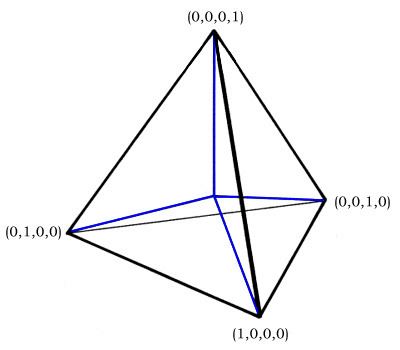
The four basis vectors stem from the center of a regular tetrahedron and go to its four corners. Their coordinate addresses are (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) and (0, 0, 0, 1) respectively. These may be scaled and linearly combined to span conventional XYZ space, with at least one of the four coordinates unneeded (set to zero) in any given quadrant.
The normalization scheme is somewhat unusual in keeping all coordinates non-negative. Typical of coordinate systems of this type (a, a, a, a) is an identity vector and may be added to normalize a result. To negate (1,0,0,0), write (−1, 0, 0, 0) then add (1, 1, 1, 1) to get (0, 1, 1, 1).
Pedagogical significance
A typical application might set the edges of the basis tetrahedron as unit, with the quadrays considered unit on some other scale. The tetrahedron itself may also be defined as the unit of volume, although the infrastructure does not demand using this setting.
The four quadrays may be linearly combined to provide integer coordinates for the inverse tetrahedron (0,1,1,1), (1,0,1,1), (1,1,0,1), (1,1,1,0), and for the cube, octahedron, rhombic dodecahedron and cuboctahedron of volumes 3, 4, 6 and 20 respectively, given the starting tetrahedron of unit volume.
For example, given A, B, C, D as (1,0,0,0), (0,1,0,0), (0,0,1,0) and (0,0,0,1) respectively, the vertices of an octahedron with the same edge length and volume four would be A + B, A + C, A + D, B + C, B + D, C + D or all eight permutations of {1,1,0,0}. The vertices of the volume 20 cuboctahedron are all 12 permutations of {2,1,1,0}.
If one now calls this volume "4D" as in "four-dimensional" or "four-directional" we have primed the pump for an understanding of R. Buckminster Fuller's "4D geometry," or Synergetics.
