 | ||
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form
where P is pressure, ρ is density and K is a constant of proportionality. The constant n is known as the polytropic index. The polytropic exponent γ = (n+1)/n is sometimes preferred over n. This relation need not be interpreted as an equation of state, although a gas following such an equation of state does produce a polytropic solution to the Lane–Emden equation. Rather, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation.
Sometimes the word polytrope may be used to refer to an equation of state that looks similar to the thermodynamic relation above, although this is potentially confusing and is to be avoided. It is preferable to refer to the fluid itself (as opposed to the solution of the Lane–Emden equation) as a polytropic fluid. The equation of state of a polytropic fluid is general enough that such idealized fluids find wide use outside of the limited problem of polytropes.
The polytropic index has been shown to be equivalent to the pressure derivative of the bulk modulus where its relation to the Murnaghan equation of state has also been demonstrated. The polytrope relation is therefore best suited for relatively low-pressure (below 107 pascals) and high-pressure (over 1014 pascals) conditions when the pressure derivative of the bulk modulus, which is equivalent to the polytrope index, is near constant.
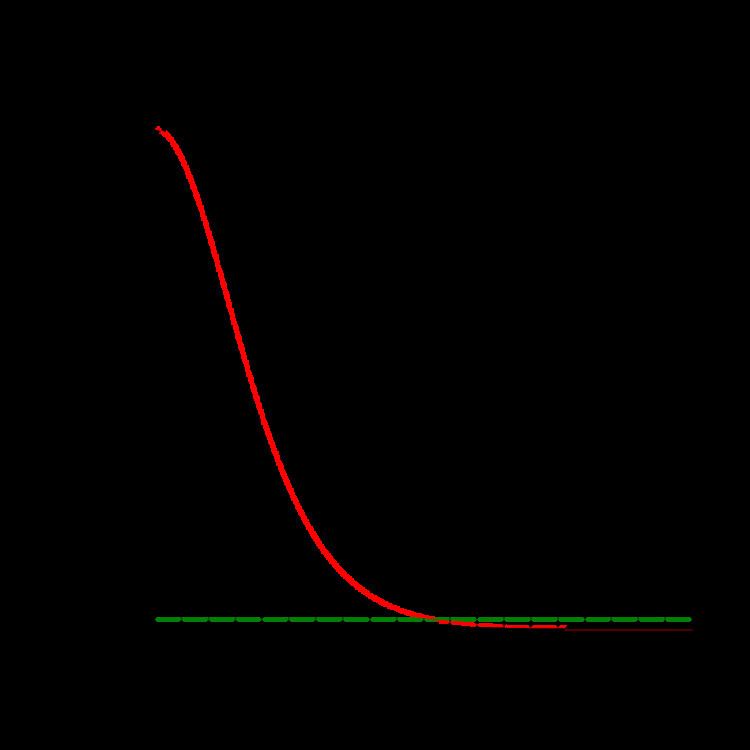
Example models by polytropic index
In general as the polytropic index increases, the density distribution is more heavily weighted toward the center (r = 0) of the body.
