Plane stress - Alchetron, The Free Social Encyclopedia

In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular surface. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2 (representable as a 2 × 2 matrix rather than 3 × 3). A related notion, plane strain, is often applicable to very thick members.

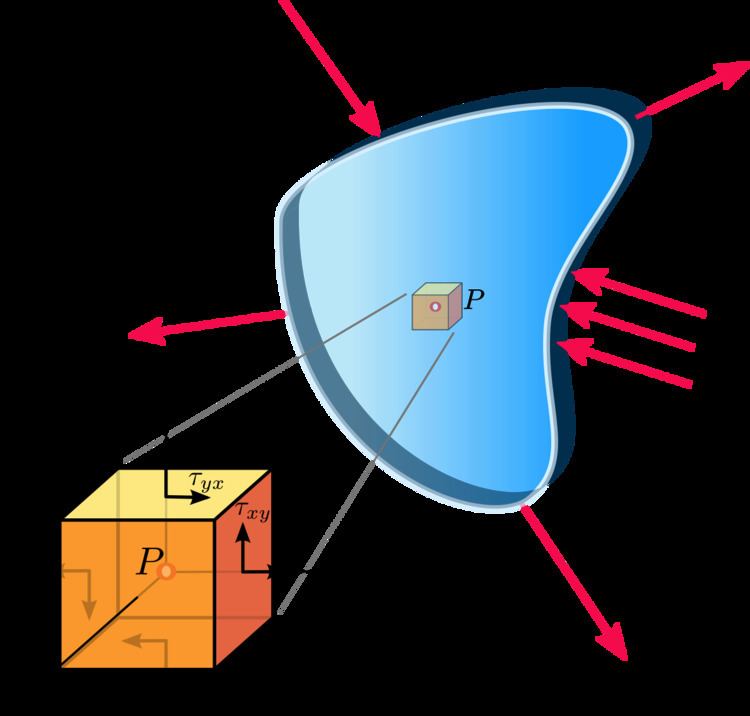
Plane stress typically occurs in thin flat plates that are acted upon only by load forces that are parallel to them. In certain situations, a gently curved thin plate may also be assumed to have plane stress for the purpose of stress analysis. This is the case, for example, of a thin-walled cylinder filled with a fluid under pressure. In such cases, stress components perpendicular to the plate are negligible compared to those parallel to it.

In other situations, however, the bending stress of a thin plate cannot be neglected. One can still simplify the analysis by using a two-dimensional domain, but the plane stress tensor at each point must be complemented with bending terms.

Mathematical definition

Mathematically, the stress at some point in the material is a plane stress if one of the three principal stresses (the eigenvalues of the Cauchy stress tensor) is zero. That is, there is Cartesian coordinate system in which the stress tensor has the form

σ = [ σ 11 0 0 0 σ 22 0 0 0 0 ] ≡ [ σ x 0 0 0 σ y 0 0 0 0 ]

For example, consider a rectangular block of material measuring 10, 40 and 5 cm along the x , y , and z , that is being stretched in the x direction and compressed in the y direction, by pairs of opposite forces with magnitudes 10 N and 20 N, respectively, uniformly distributed over the corresponding faces. The stress tensor inside the block will be

σ = [ 500 P a 0 0 0 − 4000 P a 0 0 0 0 ]

More generally, if one chooses the first two coordinate axes arbitrarily but perpendicular to the direction of zero stress, the stress tensor will have the form

σ = [ σ 11 σ 12 0 σ 21 σ 22 0 0 0 0 ] ≡ [ σ x τ x y 0 τ y x σ y 0 0 0 0 ]

and can therefore be represented by a 2 × 2 matrix,

σ i j = [ σ 11 σ 12 σ 21 σ 22 ] ≡ [ σ x τ x y τ y x σ y ]

Constitutive equations

See Hooke's law#Plane_stress

Plane stress in curved surfaces

In certain cases, the plane stress model can be used in the analysis of gently curved surfaces. For example, consider a thin-walled cylinder subjected to an axial compressive load uniformly distributed along its rim, and filled with a pressurized fluid. The internal pressure will generate a reactive hoop stress on the wall, a normal tensile stress directed perpendicular to the cylinder axis and tangential to its surface. The cylinder can be conceptually unrolled and analyzed as a flat thin rectangular plate subjected to tensile load in one direction and compressive load in another other direction, both parallel to the plate.

Plane strain (strain matrix)

If one dimension is very large compared to the others, the principal strain in the direction of the longest dimension is constrained and can be assumed as zero, yielding a plane strain condition (Figure 7.2). In this case, though all principal stresses are non-zero, the principal stress in the direction of the longest dimension can be disregarded for calculations. Thus, allowing a two dimensional analysis of stresses, e.g. a dam analyzed at a cross section loaded by the reservoir.

The corresponding strain tensor is:

ε i j = [ ε 11 ε 12 0 ε 21 ε 22 0 0 0 ε 33 ]

in which the non-zero ε 33 term arises from the Poisson's effect. This strain term can be temporarily removed from the stress analysis to leave only the in-plane terms, effectively reducing the analysis to two dimensions.

Stress transformation in plane stress and plane strain

Consider a point P in a continuum under a state of plane stress, or plane strain, with stress components ( σ x , σ y , τ x y ) and all other stress components equal to zero (Figure 8.1). From static equilibrium of an infinitesimal material element at P (Figure 8.2), the normal stress σ n and the shear stress τ n on any plane perpendicular to the x - y plane passing through P with a unit vector n making an angle of θ with the horizontal, i.e. cos ⁡ θ is the direction cosine in the x direction, is given by:

σ n = 1 2 ( σ x + σ y ) + 1 2 ( σ x − σ y ) cos ⁡ 2 θ + τ x y sin ⁡ 2 θ τ n = − 1 2 ( σ x − σ y ) sin ⁡ 2 θ + τ x y cos ⁡ 2 θ

These equations indicate that in a plane stress or plane strain condition, one can determine the stress components at a point on all directions, i.e. as a function of θ , if one knows the stress components ( σ x , σ y , τ x y ) on any two perpendicular directions at that point. It is important to remember that we are considering a unit area of the infinitesimal element in the direction parallel to the y - z plane.

The principal directions (Figure 8.3), i.e., orientation of the planes where the shear stress components are zero, can be obtained by making the previous equation for the shear stress τ n equal to zero. Thus we have:

τ n = − 1 2 ( σ x − σ y ) sin ⁡ 2 θ + τ x y cos ⁡ 2 θ = 0

and we obtain

tan ⁡ 2 θ p = 2 τ x y σ x − σ y

This equation defines two values θ p which are 90 ∘ apart (Figure 8.3). The same result can be obtained by finding the angle θ which makes the normal stress σ n a maximum, i.e. d σ n d θ = 0

The principal stresses σ 1 and σ 2 , or minimum and maximum normal stresses σ m a x and σ m i n , respectively, can then be obtained by replacing both values of θ p into the previous equation for σ n . This can be achieved by rearranging the equations for σ n and τ n , first transposing the first term in the first equation and squaring both sides of each of the equations then adding them. Thus we have

[ σ n − 1 2 ( σ x + σ y ) ] 2 + τ n 2 = [ 1 2 ( σ x − σ y ) ] 2 + τ x y 2 ( σ n − σ a v g ) 2 + τ n 2 = R 2

where

R = [ 1 2 ( σ x − σ y ) ] 2 + τ x y 2 and σ a v g = 1 2 ( σ x + σ y )

which is the equation of a circle of radius R centered at a point with coordinates [ σ a v g , 0 ] , called Mohr's circle. But knowing that for the principal stresses the shear stress τ n = 0 , then we obtain from this equation:

σ 1 = σ m a x = 1 2 ( σ x + σ y ) + [ 1 2 ( σ x − σ y ) ] 2 + τ x y 2 σ 2 = σ m i n = 1 2 ( σ x + σ y ) − [ 1 2 ( σ x − σ y ) ] 2 + τ x y 2

When τ x y = 0 the infinitesimal element is oriented in the direction of the principal planes, thus the stresses acting on the rectangular element are principal stresses: σ x = σ 1 and σ y = σ 2 . Then the normal stress σ n and shear stress τ n as a function of the principal stresses can be determined by making τ x y = 0 . Thus we have

σ n = 1 2 ( σ 1 + σ 2 ) + 1 2 ( σ 1 − σ 2 ) cos ⁡ 2 θ τ n = − 1 2 ( σ 1 − σ 2 ) sin ⁡ 2 θ

Then the maximum shear stress τ m a x occurs when sin ⁡ 2 θ = 1 , i.e. θ = 45 ∘ (Figure 8.3):

τ m a x = 1 2 ( σ 1 − σ 2 )

Then the minimum shear stress τ m i n occurs when sin ⁡ 2 θ = − 1 , i.e. θ = 135 ∘ (Figure 8.3):

τ m i n = − 1 2 ( σ 1 − σ 2 )

References

Plane stress Wikipedia

(Text) CC BY-SA