Pairing based cryptography

Definition

The following definition is commonly used in most academic papers.

Let G 1 , G 2 be two additive cyclic groups of prime order q , and G T another cyclic group of order q written multiplicatively. A pairing is a map: e : G 1 × G 2 → G T , which satisfies the following properties:

1. Bilinearity: ∀ a , b ∈ F q ∗ ,   ∀ P ∈ G 1 , Q ∈ G 2 :   e ( a P , b Q ) = e ( P , Q ) a b
2. Non-degeneracy: e ≠ 1
3. Computability: there exist an efficient algorithm to compute e .

Classification

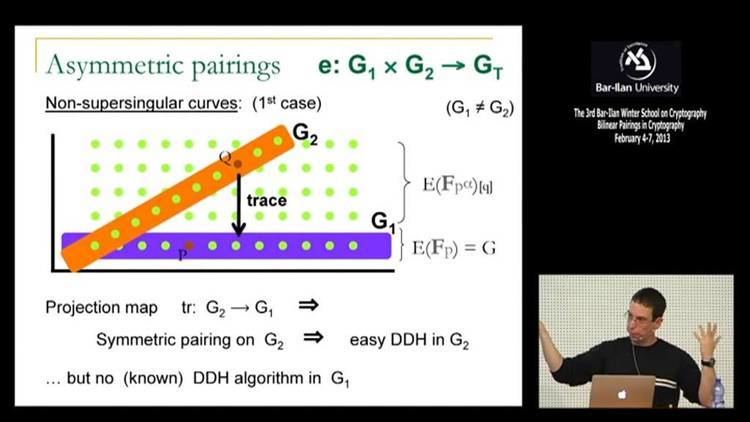
If the same group is used for the first two groups (i.e. G 1 = G 2 ), the pairing is called symmetric and is a mapping from two elements of one group to an element from a second group.

Some researchers classify pairing instantiations into three (or more) basic types:

Usage in cryptography

If symmetric, pairings can be used to reduce a hard problem in one group to a different, usually easier problem in another group.

For example, in groups equipped with a bilinear mapping such as the Weil pairing or Tate pairing, generalizations of the computational Diffie–Hellman problem are believed to be infeasible while the simpler decisional Diffie–Hellman problem can be easily solved using the pairing function. The first group is sometimes referred to as a Gap Group because of the assumed difference in difficulty between these two problems in the group.

While first used for cryptanalysis, pairings have also been used to construct many cryptographic systems for which no other efficient implementation is known, such as identity based encryption or attribute based encryption schemes.

A contemporary example of using bilinear pairings is exemplified in the Boneh-Lynn-Shacham signature scheme.

Cryptanalysis

In June 2012 the National Institute of Information and Communications Technology (NICT), Kyushu University, and Fujitsu Laboratories Limited improved the previous bound for successfully computing a discrete logarithm on a supersingular elliptic curve from 676 bits to 923 bits.