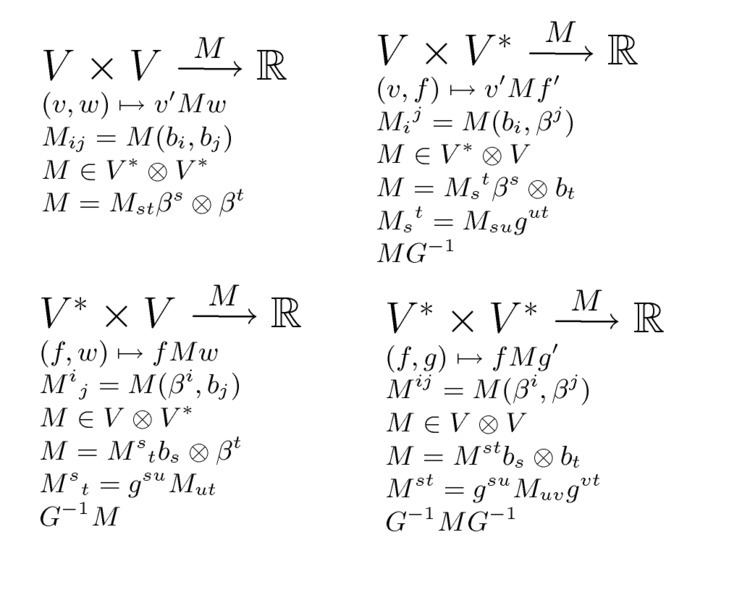Neha Patil (Editor)

Bilinear map

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Bilinear map

In mathematics, a bilinear map is a function combining elements of two vector spaces to yield an element of a third vector space, and is linear in each of its arguments. Matrix multiplication is an example.

Contents

Vector spaces

Let V, W and X be three vector spaces over the same base field F. A bilinear map is a function

B : V × W → X

such that for any w in W the map

v ↦ B(v, w)

is a linear map from V to X, and for any v in V the map

w ↦ B(v, w)

is a linear map from W to X.

In other words, when we hold the first entry of the bilinear map fixed while letting the second entry vary, the result is a linear operator, and similarly for when we hold the second entry fixed.

If V = W and we have B(v, w) = B(w, v) for all v, w in V, then we say that B is symmetric.

The case where X is the base field F, and we have a bilinear form, is particularly useful (see for example scalar product, inner product and quadratic form).

Modules

The definition works without any changes if instead of vector spaces over a field F, we use modules over a commutative ring R. It generalizes to n-ary functions, where the proper term is multilinear.

For non-commutative rings R and S, a left R-module M and a right S-module N, a bilinear map is a map B : M × N → T with T an (R, S)-bimodule, and for which any n in N, m ↦ B(m, n) is an R-module homomorphism, and for any m in M, n ↦ B(m, n) is an S-module homomorphism. This satisfies

B(r ⋅ m, n) = r ⋅ B(m, n)B(m, n ⋅ s) = B(m, n) ⋅ s

for all m in M, n in N, r in R and s in S, as well as B being additive in each argument.

Properties

A first immediate consequence of the definition is that B(v, w) = 0X whenever v = 0V or w = 0W. This may be seen by writing the zero vector 0X as 0 ⋅ 0X (and similarly for 0W) and moving the scalar 0 "outside", in front of B, by linearity.

The set L(V, W; X) of all bilinear maps is a linear subspace of the space (viz. vector space, module) of all maps from V × W into X.

If V, W, X are finite-dimensional, then so is L(V, W; X). For X = F, i.e. bilinear forms, the dimension of this space is dim V × dim W (while the space L(V × W; F) of linear forms is of dimension dim V + dim W). To see this, choose a basis for V and W; then each bilinear map can be uniquely represented by the matrix B(ei, fj), and vice versa. Now, if X is a space of higher dimension, we obviously have dim L(V, W; X) = dim V × dim W × dim X.

Examples

  • Matrix multiplication is a bilinear map M(m, n) × M(n, p) → M(m, p).
  • If a vector space V over the real numbers R carries an inner product, then the inner product is a bilinear map V × V → R.
  • In general, for a vector space V over a field F, a bilinear form on V is the same as a bilinear map V × V → F.
  • If V is a vector space with dual space V∗, then the application operator, b(f, v) = f(v) is a bilinear map from V∗ × V to the base field.
  • Let V and W be vector spaces over the same base field F. If f is a member of V∗ and g a member of W∗, then b(v, w) = f(v)g(w) defines a bilinear map V × W → F.
  • The cross product in R3 is a bilinear map R3 × R3 → R3.
  • Let B : V × W → X be a bilinear map, and L : U → W be a linear map, then (v, u) ↦ B(v, Lu) is a bilinear map on V × U.

    • References

    Bilinear map Wikipedia
    (Text) CC BY-SA


    Similar Topics