Puneet Varma (Editor)

Overlap–save method

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Overlap–save method

Overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal x [ n ] and a finite impulse response (FIR) filter h [ n ] :

Contents

where h[m]=0 for m outside the region [1, M].

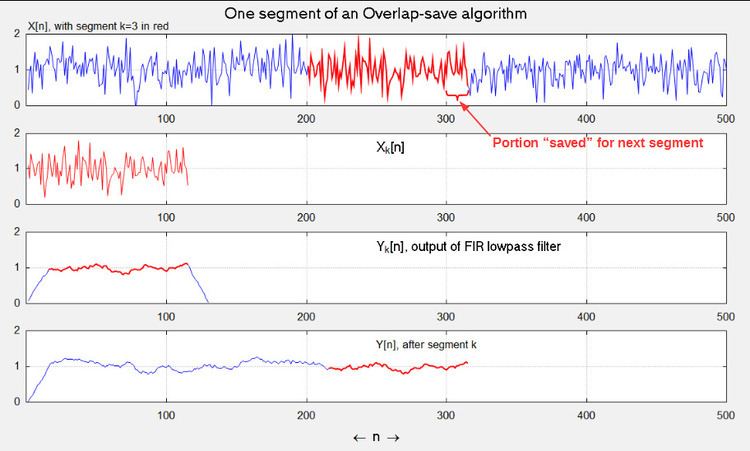
The concept is to compute short segments of y[n] of an arbitrary length L, and concatenate the segments together. Consider a segment that begins at n = kL + M, for any integer k, and define:

x k [ n ]   = d e f { x [ n + k L ] 1 ≤ n ≤ L + M − 1 0 otherwise . y k [ n ]   = d e f   x k [ n ] ∗ h [ n ]

Then, for kL + M  ≤  n  ≤  kL + L + M − 1, and equivalently M  ≤  n − kL  ≤  L + M − 1, we can write:

y [ n ] = ∑ m = 1 M h [ m ] ⋅ x k [ n − k L − m ] = x k [ n − k L ] ∗ h [ n ] = d e f   y k [ n − k L ] .

The task is thereby reduced to computing yk[n], for M  ≤  n  ≤  L + M − 1. The process described above is illustrated in the accompanying figure.

Now note that if we periodically extend xk[n] with period N  ≥  L + M − 1, according to:

x k , N [ n ]   = d e f   ∑ ℓ = − ∞ ∞ x k [ n − ℓ N ] ,

the convolutions   ( x k , N ) ∗ h   and   x k ∗ h   are equivalent in the region M  ≤  n  ≤  L + M − 1. So it is sufficient to compute the N-point circular (or cyclic) convolution of x k [ n ] with h [ n ]   in the region [1, N].  The subregion [M, L + M − 1] is appended to the output stream, and the other values are discarded.

The advantage is that the circular convolution can be computed very efficiently as follows, according to the circular convolution theorem:

y k [ n ] = DFT − 1 (   DFT ( x k [ n ] ) ⋅ DFT ( h [ n ] )   ) ,

where:

  • DFT and DFT−1 refer to the Discrete Fourier transform and inverse Discrete Fourier transform, respectively, evaluated over N discrete points, and
  • N is customarily chosen to be an integer power-of-2, which optimizes the efficiency of the FFT algorithm.
  • Optimal N is in the range [4M, 8M].
  • Unlike the third graph in the figure above, depicting separate leading and trailing edge-effects, this method causes them to be overlapped and added. So they are discarded together.

    • Pseudocode

    (Overlap–save algorithm for linear convolution) h = FIR_impulse_response M = length(h) overlap = M-1 N = 4*overlap (or a nearby power-of-2) step_size = N-overlap H = DFT(h, N) position = 0 while position+N <= length(x) yt = IDFT( DFT( x(1+position : N+position), N ) * H, N ) y(1+position : step_size+position) = yt(M : N) #discard M-1 y-values position = position + step_size end

    Efficiency

    When the DFT and its inverse is implemented by the FFT algorithm, the pseudocode above requires about N log2(N) + N complex multiplications for the FFT, product of arrays, and IFFT. Each iteration produces N-M+1 output samples, so the number of complex multiplications per output sample is about:

    For example, when M=201 and N=1024, Eq.2 equals 13.67, whereas direct evaluation of Eq.1 would require up to 201 complex multiplications per output sample, the worst case being when both x and h are complex-valued. Also note that for any given M, Eq.2 has a minimum with respect to N. It diverges for both small and large block sizes.

    Overlap–discard

    Overlap–discard and Overlap–scrap are less commonly used labels for the same method described here. However, these labels are actually better (than overlap–save) to distinguish from overlap–add, because both methods "save", but only one discards. "Save" merely refers to the fact that M − 1 input (or output) samples from segment k are needed to process segment k + 1.

    Extending overlap–save

    The overlap-save algorithm may be extended to include other common operations of a system:

  • additional channels can be processed more cheaply than the first by reusing the forward FFT
  • sampling rates can be changed by using different sized forward and inverse FFTs
  • frequency translation (mixing) can be accomplished by rearranging frequency bins

    • References

    Overlap–save method Wikipedia
    (Text) CC BY-SA