Orbital angular momentum of light

Introduction

A beam of light carries a linear momentum P , and hence it can be also attributed an external angular momentum L e = r × P . This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated to polarization and depends on the spatial distribution of the optical field (E).

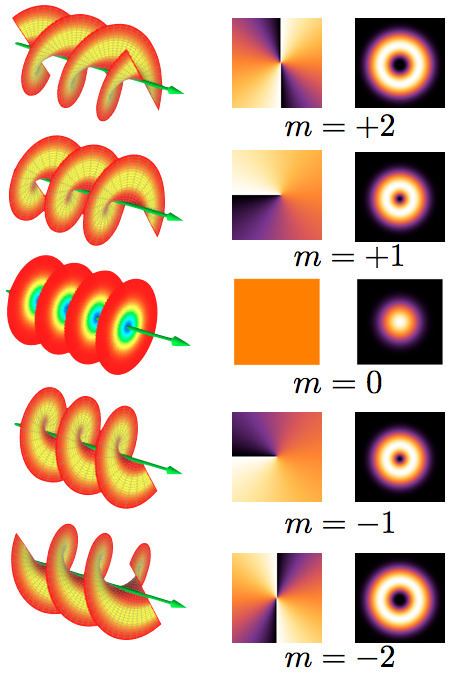
A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called "helical mode". Helical modes of the electromagnetic field are characterized by a wavefront that is shaped as a helix, with an optical vortex in the center, at the beam axis (see figure). The helical modes are characterized by an integer number m , positive or negative. If m = 0 , the mode is not helical and the wavefronts are multiple disconnected surfaces, for example, a sequence of parallel planes (from which the name "plane wave"). If m = ± 1 , the handedness determined by the sign of m , the wavefront is shaped as a single helical surface, with a step length equal to the wavelength λ . If | m | ⩾ 2 , the wavefront is composed of | m | distinct but intertwined helices, with the step length of each helix surface equal to | m | λ , and a handedness given by the sign of m . The integer m is also the so-called "topological charge" of the optical vortex. Light beams that are in a helical mode carry nonzero OAM.

In the figure to the right, the first column shows the beam wavefront shape. The second column is the optical phase distribution in a beam cross-section, shown in false colors. The third column is the light intensity distribution in a beam cross-section (with a dark vortex core at the center).

Photons corresponding to such a beam each have an OAM of m ℏ directed along the beam axis. This OAM is origin-independent.

As an example, any Laguerre-Gaussian mode with rotational mode number l≠0 has such a helical wavefront.

Mathematical expressions for the orbital angular momentum of light

The classical expression of the orbital angular momentum in the paraxial limit is the following:

where E and A are the electric field and the vector potential, respectively, ϵ 0 is the vacuum permittivity and we are using SI units. The i -superscripted symbols denote the cartesian components of the corresponding vectors.

For a monochromatic wave this expression can be transformed into the following one:

This expression is generally nonvanishing when the wave is not cylindrically symmetric. In particular, in a quantum theory, individual photons may have the following values of the OAM:

The corresponding wave functions (eigenfunctions of OAM operator) have the following general expression:

where ϕ is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.

Production of OAM states

Orbital angular momentum states with l = ± 1 occur naturally, there are a number of ways of creating OAM states of arbitrary l in the lab including via spiral phase plates, spatial light modulators and q-plates.

Spiral wave plates, made of plastic or glass, are plates where the thickness of the material increases in a spiral pattern in order to imprint a phase gradient on light passing through it. For a given wavelength, an OAM state of a given l requires that the step height, the height between the thinnest and thickest parts of the plate be given by s = l λ / ( n − 1 ) where n is an integer. Although the wave plates themselves are efficient, they are relatively expensive and are, in general, not adjustable to different wavelengths of light.

Another way to modify the phase of the light is with a diffraction grating. For an l = 0 state, the diffraction grating would consist of parallel lines. However, for an l = 1 state, there will be a "fork" dislocation, and the number of lines above the dislocation will be one larger than below. An OAM state with l > 1 can be created by increasing the difference in the number of lines above and below the dislocation. As with the spiral wave plates, these diffraction gratings are fixed for l , but are not restricted to a particular wavelength. A spatial light modulator operates in a similar way to the diffraction grating, but can be controlled by computer to dynamically generate a wide range of OAM states.

Theoretical work suggests that a series of optically distinct chromophores are capable of supporting an excitonic state whose symmetry is such that in the course of the exciton relaxing, a radiation mode of non-zero topological charge is created directly.

Most recently, the geometric phase concept is adopted for OAM generation. The geometric phase is modulated to coincide with the spatial phase dependence factor, i.e., e i m ϕ of an OAM carrying wave. In this way, geometric phase is introduced by using anisotropic scatterers. For example, a metamaterial composed of distributed linear polarizers in a rotational symmetric manner generates an OAM of order 1. To generate higher-order OAM wave, nano-antennas which can bring the spin-obit coupling effect are designed and then arranged to form a metasurface with different topological charges. Consequently, the transmitted wave carries an OAM and its order is twice the value of the topological charge. Usually, the conversion efficiency is not high for the transmission-type metasurface. Alternative solution to achieve high transmittance is to use complementary (Babinet-inverted) metasurface. On the other hand, it is much easier to achieve high conversion efficiency, even 100% efficiency in the reflection-type metasurface such as the composite PEC-PMC metasurface.

Potential use in telecommunications

Research into OAM has suggested that light waves could carry hitherto unprecedented quantities of data through optical fibres. According to preliminary tests, data streams travelling along a beam of light split into 8 different circular polarities have demonstrated the capacity to transfer up to 2.5 terabits of data (equivalent to 66 DVDs or 320 Gigabytes) per second. Further research into OAM multiplexing in the radio and mm wavelength frequencies has been shown in preliminary tests to be able to transmit 32 gigabits of data per second over the air. There is an ongoing discussion if this will add any capacity on top of other schemes, such as MIMO.

Measuring the orbital angular momentum of light

Determining the spin angular momentum (SAM) of light is simple – SAM is related to the polarization state of the light: the AM is, per photon, in a left and right circularly polarized beam respectively. Thus the SAM can be measured by transforming the circular polarization of light into a p- or s-polarized state by means of a wave plate and then using a polarizing beam splitter that will transmit or reflect the state of light.

The development of a simple and reliable method for the measurement of orbital angular momentum (OAM) of light, however, remains an important problem in the field of light manipulation. OAM (per photon) arises from the amplitude cross-section of the beam and is therefore independent of the spin angular momentum: whereas SAM has only two orthogonal states, the OAM is described by a state that can take any integer value N. As the state of OAM of light is unbounded, any integer value of l is orthogonal to (independent from) all the others. Where a beam splitter could separate the two states of SAM, no device can separate the N (if greater than 2) modes of OAM, and, clearly, the perfect detection of all N potential states is required to finally resolve the issue of measuring OAM.

Nevertheless, some methods have been investigated for the measurement of OAM.

Counting spiral fringes

Beams carrying OAM have a helical phase structure. Interfering such a beam with a uniform plane wave allows to reveal phase information about the input beam through analysis of the observed spiral fringes. In a Mach–Zender interferometer, a helically phased source beam is made to interfere with a plane-wave reference beam along a collinear path. Interference fringes will be observed in the plane of the beam waist and/or at the Rayleigh range. The path being collinear, these fringes are pure consequence of the relative phase structure of the source beam. Each fringe in the pattern corresponds to one step through: counting the fringes suffices to determine the value of l.

Diffractive holographic filters

Computer-generated holograms can be used to generate beams containing phase singularities, and these have now become a standard tool for the generation of beams carrying OAM. This generating method can be reversed: the hologram, coupled to a single-mode fiber of set entrance aperture, becomes a filter for OAM. This approach is widely used for the detection of OAM at the single-photon level.

These holograms are the phase of the product of the vortex term and a phase-ramp term filtered such that points whose phase is in the lower half of all possible phase values are colored white, and the remainder are colored white. This filtering process is referred to as blazing and results in distributing the phase into all possible diffraction orders.

Other methods

Other methods to measure the OAM of light include the rotational Doppler effect, systems based on a Dove prism interferometer, optical transformations, the measure of the spin of trapped particles, and the study of diffraction effects from apertures.

Quantum-information applications

OAM states can be generated in coherent superpositions and they can be entangled, which is an integral element of schemes for quantum information protocols. These states can be generated using parametric down-conversion, and correlations measured using spatial light modulators (SLM). Using qudits (with d levels, as opposed to a qubit's 2 levels) has been shown to improve the robustness of quantum key distribution schemes. OAM states provide a suitable physical realisation of such a system, and a proof-of-principle experiment (with 7 OAM modes from l = − 3 to l = 3 ) has been demonstrated.