 | ||
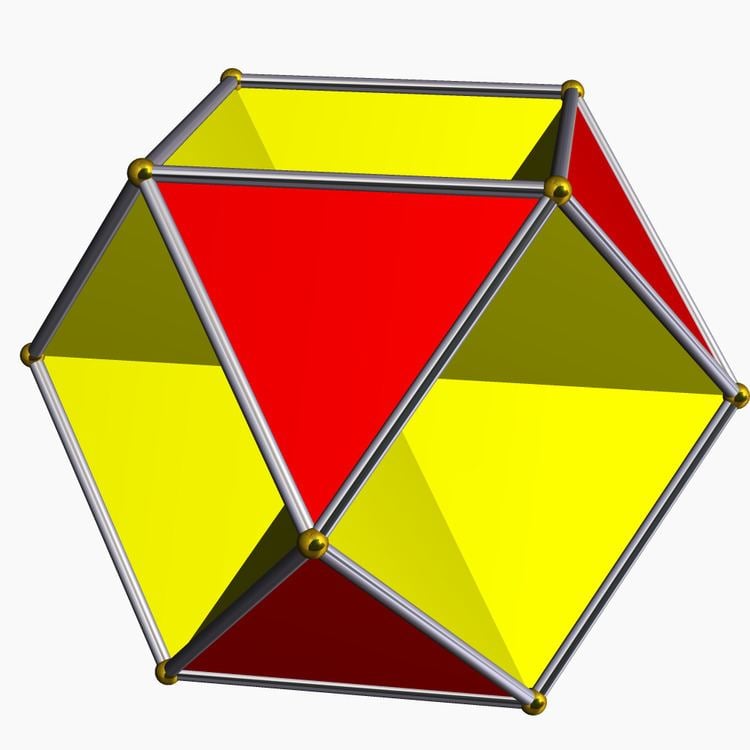
In geometry, the octahemioctahedron or allelotetratetrahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.
Contents
It is one of nine hemipolyhedra, with 4 hexagonal faces passing through the model center.
Orientability
It is the only hemipolyhedron that is orientable, and the only uniform polyhedron with an Euler characteristic of zero (a topological torus).
Related polyhedra
It shares the vertex arrangement and edge arrangement with the cuboctahedron (having the triangular faces in common), and with the cubohemioctahedron (having the hexagonal faces in common).
By Wythoff construction it has tetrahedral symmetry (Td), like the rhombitetratetrahedron construction for the cuboctahedron, with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetry (Oh).
Octahemioctacron
The octahemioctacron is the dual of the octahemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the hexahemioctacron.
Since the hemipolyhedra have faces passing through the center, the dual figures have corresponding vertices at infinity; properly, on the real projective plane at infinity. In Magnus Wenninger's Dual Models, they are represented with intersecting prisms, each extending in both directions to the same vertex at infinity, in order to maintain symmetry. In practice the model prisms are cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation figures, called stellation to infinity. However, he also suggested that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
The octahemioctacron has four vertices at infinity.
