Hexagon

Regular hexagon

A regular hexagon has Schläfli symbol {6} and can also be constructed as a truncated equilateral triangle, t{3}, which alternates two types of edges.

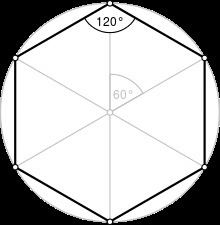
A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle).

The common length of the sides equals the radius of the circumscribed circle, which equals 2 3 3 times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has 6 rotational symmetries (rotational symmetry of order six) and 6 reflection symmetries (six lines of symmetry), making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.

Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.

Parameters

The maximal diameter, D is twice the maximal radius or circumradius, R, which equals the side length, t. The minimal diameter or the diameter of the inscribed circle (separation of parallel sides, flat-to-flat distance, or height when resting on a flat base), d, is twice the minimal radius or inradius, r. The maxima and minima are related by the same factor:

The area of a regular hexagon

For any regular polygon, the area can also be expressed in terms of the apothem, a = r, and perimeter, p = 6 R = 4 r 3 :

The regular hexagon fills the fraction 3 3 2 π ≈ 0.8270 of its circumscribed circle.

If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumscribing circle between B and C, then PE + PF = PA + PB + PC + PD.

Symmetry

The regular hexagon has Dih₆ symmetry, order 12. There are 3 dihedral subgroups: Dih₃, Dih₂, and Dih₁, and 4 cyclic subgroups: Z₆, Z₃, Z₂, and Z₁.

These symmetries express 9 distinct symmetries of a regular hexagon. John Conway labels these by a letter and group order. r12 is full symmetry, and a1 is no symmetry. d6, a isogonal hexagon constructed by four mirrors can alternate long and short edges, and p6, an isotoxal hexagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular hexagon. The i4 forms are regular hexagons flattened or stretched along one symmetry direction. It can be seen as an elongated rhombus, while d2 and p2 can be seen as horizontally and vertically elongated kites. g2 hexagons, with opposite sides parallel are also called hexagonal parallelogons.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g6 subgroup has no degrees of freedom but can seen as directed edges.

Hexagons of symmetry g2, i4, and r12, as parallelogons can tessellate the Euclidean plane by translation. Other hexagon shapes can tile the plane with different orientations.

Related polygons and tilings

A regular hexagon has Schläfli symbol {6}. A regular hexagon is a part the regular hexagonal tiling, {6,3}, with 3 hexagonal around each vertex.

A regular hexagon can also be created as a truncated equilateral triangle, with Schläfli symbol t{3}. Seen with two types (colors) of edges, this form only has D₃ symmetry.

A truncated hexagon, t{6}, is an dodecagon, {12}, alternating 2 types (colors) of edges. An alternated hexagon, h{6}, is a equilateral triangle, {3}. A regular hexagon can be stellated with equilateral triangles on its edges, creating a hexagram. A regular hexagon can be dissected into 6 equilateral triangles by adding a center point. This pattern repeats within the regular triangular tiling.

A regular hexagon can be extended into a regular dodecagon by adding alternating squares and equilateral triangles around it. This pattern repeats within the rhombitrihexagonal tiling.

Hexagonal structures

From bees' honeycombs to the Giant's Causeway, hexagonal patterns are prevalent in nature due to their efficiency. In a hexagonal grid each line is as short as it can possibly be if a large area is to be filled with the fewest number of hexagons. This means that honeycombs require less wax to construct and gain lots of strength under compression.

Irregular hexagons with parallel opposite edges are called parallelogons and can also tile the plane by translation. In three dimensions, hexagonal prisms with parallel opposite faces are called parallelohedrons and these can tessellate 3-space by translation.

Tesselations by hexagons

In addition to the regular hexagon, which determines a unique tessellation of the plane, any irregular hexagon which satisfies the Conway criterion will tile the plane.

Hexagon inscribed in a conic section

Pascal's theorem (also known as the "Hexagrammum Mysticum Theorem") states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the "Pascal line" of that configuration.

Cyclic hexagon

The Lemoine hexagon is a cyclic hexagon (one inscribed in a circle) with vertices given by the six intersections of the edges of a triangle and the three lines that are parallel to the edges that pass through its symmedian point.

If the successive sides of a cyclic hexagon are a, b, c, d, e, f, then the three main diagonals intersect in a single point if and only if ace = bdf.

If, for each side of a cyclic hexagon, the adjacent sides are extended to their intersection, forming a triangle exterior to the given side, then the segments connecting the circumcenters of opposite triangles are concurrent.

If a hexagon has vertices on the circumcircle of an acute triangle at the six points (including three triangle vertices) where the extended altitudes of the triangle meet the circumcircle, then the area of the hexagon is twice the area of the triangle.

Hexagon tangential to a conic section

Let ABCDEF be a hexagon formed by six tangent lines of a conic section. Then Brianchon's theorem states that the three main diagonals AD, BE, and CF intersect at a single point.

In a hexagon that is tangential to a circle and that has consecutive sides a, b, c, d, e, and f,

Equilateral triangles on the sides of an arbitrary hexagon

If an equilateral triangle is constructed externally on each side of any hexagon, then the midpoints of the segments connecting the centroids of opposite triangles form another equilateral triangle.

Skew hexagon

A skew hexagon is a skew polygon with 6 vertices and edges but not existing on the same plane. The interior of such an hexagon is not generally defined. A skew zig-zag hexagon has vertices alternating between two parallel planes.

A regular skew hexagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew hexagon and can be seen in the vertices and side edges of a triangular antiprism with the same D_3d, [2⁺,6] symmetry, order 12.

The cube and octahedron (same as triangular antiprism) have regular skew hexagons as petrie polygons.

Petrie polygons

The regular skew hexagon is the Petrie polygon for these higher dimensional regular, uniform and dual polyhedra and polytopes, shown in these skew orthogonal projections:

Convex equilateral hexagon

A principal diagonal of a hexagon is a diagonal which divides the hexagon into quadrilaterals. In any convex equilateral hexagon (one with all sides equal) with common side a, there exists a principal diagonal d₁ such that

and a principal diagonal d₂ such that

Polyhedra with hexagons

There is no Platonic solid made of only regular hexagons, because the hexagons tessellate, not allowing the result to "fold up". The Archimedean solids with some hexagonal faces are the truncated tetrahedron, truncated octahedron, truncated icosahedron (of soccer ball and fullerene fame), truncated cuboctahedron and the truncated icosidodecahedron. These hexagons can be considered truncated triangles, with Coxeter diagrams of the form and .

There are other symmetry polyhedra with stretched or flattened hexagons, like these Goldberg polyhedron G(2,0):

There are also 9 Johnson solids with regular hexagons: