Non random two liquid model

Equations for a binary mixture

For a binary mixture the following function are used:

{ ln ⁡   γ 1 = x 2 2 [ τ 21 ( G 21 x 1 + x 2 G 21 ) 2 + τ 12 G 12 ( x 2 + x 1 G 12 ) 2 ] ln ⁡   γ 2 = x 1 2 [ τ 12 ( G 12 x 2 + x 1 G 12 ) 2 + τ 21 G 21 ( x 1 + x 2 G 21 ) 2 ]

with

{ ln ⁡   G 12 = − α 12   τ 12 ln ⁡   G 21 = − α 21   τ 21

In here τ 12 and τ 21 are the dimensionless interaction parameters, which are related to the interaction energy parameters Δ g 12 and Δ g 21 by:

{ τ 12 = Δ g 12 R T = U 12 − U 22 R T τ 21 = Δ g 21 R T = U 21 − U 11 R T

Here R is the gas constant and T the absolute temperature, and U_ij is the energy between molecular surface i and j. U_ii is the energy of evaporation. Here U_ij has to be equal to U_ji, but Δ g i j is not necessary equal to Δ g j i .

The parameters α 12 and α 21 are the so-called non-randomness parameter, for which usually α 12 is set equal to α 21 . For a liquid, in which the local distribution is random around the center molecule, the parameter α 12 = 0 . In that case the equations reduce to the one-parameter Margules activity model:

{ ln ⁡   γ 1 = x 2 2 [ τ 21 + τ 12 ] = A x 2 2 ln ⁡   γ 2 = x 1 2 [ τ 12 + τ 21 ] = A x 1 2

In practice, α 12 is set to 0.2, 0.3 or 0.48. The latter value is frequently used for aqueous systems. The high value reflects the ordered structure caused by hydrogen bonds. However, in the description of liquid-liquid equilibria the non-randomness parameter is set to 0.2 to avoid wrong liquid-liquid description. In some cases a better phase equilibria description is obtained by setting α 12 = − 1 . However this mathematical solution is impossible from a physical point of view, since no system can be more random than random ( α 12 =0). In general NRTL offers more flexibility in the description of phase equilibria than other activity models due to the extra non-randomness parameters. However, in practice this flexibility is reduced in order to avoid wrong equilibrium description outside the range of regressed data.

The limiting activity coefficients, aka the activity coefficients at infinite dilution, are calculated by:

{ ln ⁡   γ 1 ∞ = [ τ 21 + τ 12 exp ⁡ ( − α 12   τ 12 ) ] ln ⁡   γ 2 ∞ = [ τ 12 + τ 21 exp ⁡ ( − α 12   τ 21 ) ]

The expressions show that at α 12 = 0 the limiting activity coefficients are equal. This situation that occurs for molecules of equal size, but of different polarities.
It also shows, since three parameters are available, that multiple sets of solutions are possible.

General equations

The general equation for ln ⁡ ( γ i ) for species i in a mixture of n components is:

ln ⁡ ( γ i ) = ∑ j = 1 n x j τ j i G j i ∑ k = 1 n x k G k i + ∑ j = 1 n x j G i j ∑ k = 1 n x k G k j ( τ i j − ∑ m = 1 n x m τ m j G m j ∑ k = 1 n x k G k j )

with

G i j = exp ⁡ ( − α i j τ i j )

α i j = α i j 0 + α i j 1 T

τ i , j = A i j + B i j T + C i j T 2 + D i j ln ⁡ ( T ) + E i j T F i j

There are several different equation forms for α i j and τ i j , the most general of which are shown above.

Temperature dependent parameters

To describe phase equilibria over a large temperature regime, i.e. larger than 50 K, the interaction parameter has to be made temperature dependent. Two formats are frequently used. The extended Antoine equation format:

Here the logarithmic term is mainly used in the description of liquid-liquid equilibria (miscibility gap).

The other format is a second-order polynomial format:

Parameter determination

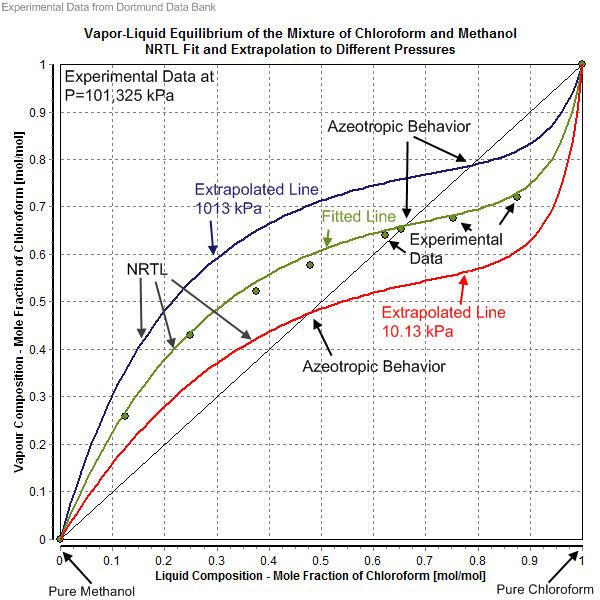
The NRTL parameters are fitted to activity coefficients that have been derived from experimentally determined phase equilibrium data (vapor–liquid, liquid–liquid, solid–liquid) as well as from heats of mixing. The source of the experimental data are often factual data banks like the Dortmund Data Bank. Other options are direct experimental work and predicted activity coefficients with UNIFAC and similar models. Noteworthy is that for the same liquid mixture several NRTL parameter sets might exist. The NRTL parameter set to use depends on the kind of phase equilibrium (i.e. solid–liquid, liquid–liquid, vapor–liquid). In the case of the description of a vapor–liquid equilibria it is necessary to know which saturated vapor pressure of the pure components was used and whether the gas phase was treated as an ideal or a real gas. Accurate saturated vapor pressure values are important in the determination or the description of an azeotrope. The gas fugacity coefficients are mostly set to unity (ideal gas assumption), but for vapor-liquid equilibria at high pressures (i.e. > 10 bar) an equation of state is needed to calculate the gas fugacity coefficient for a real gas description. Determination of NRTL parameters from LLE data is more complicated than parameter regression from VLE data as it involves solving isoactivity equations which are highly non-linear. In addition, parameters obtained from LLE may not always represent the real activity of components due to lack of knowledge on the activity values of components in the data regression.