Nephroid

Equations of a nephroid

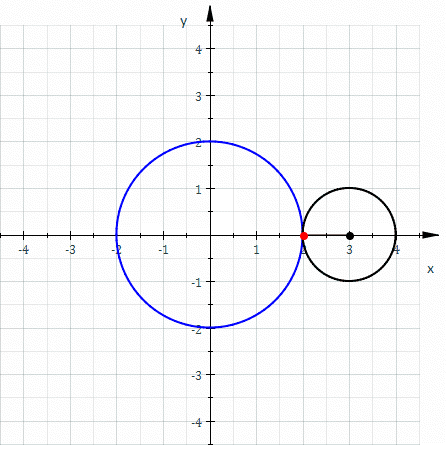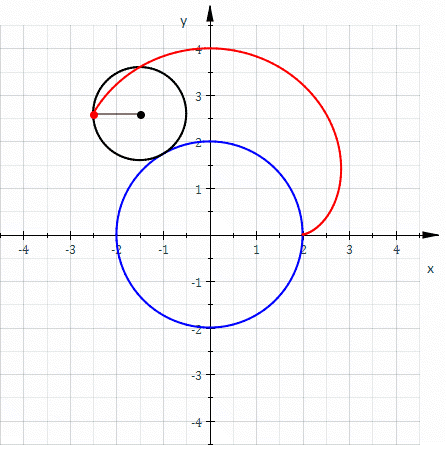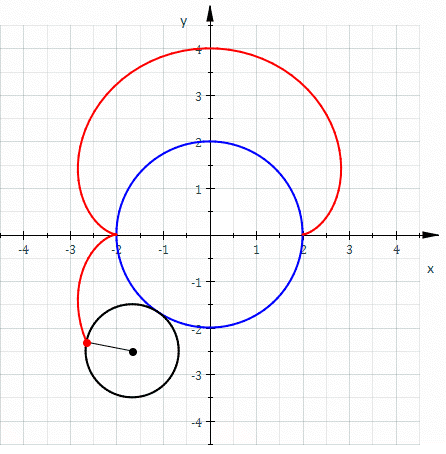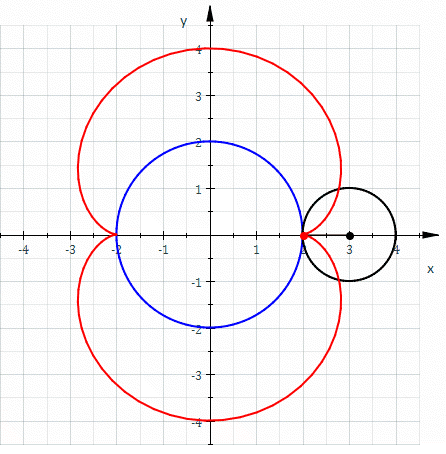
If the small circle has radius a , the fixed circle has midpoint ( 0 , 0 ) and radius 2 a , the rolling angle of the small circle is 2 φ and point ( 2 a , 0 ) the starting point (s. picture) then one gets the

parametric representation

x ( φ ) = 3 a cos ⁡ φ − a cos ⁡ 3 φ = 6 a cos ⁡ φ − 4 a cos 3 ⁡ φ   , y ( φ ) = 3 a sin ⁡ φ − a sin ⁡ 3 φ = 4 a sin 3 ⁡ φ   , 0 ≤ φ < 2 π

Inserting x ( φ ) and y ( φ ) into the equation

( x 2 + y 2 − 4 a 2 ) 3 = 108 a 4 y 2 .

shows: this equation is an implicit representation of the curve.

proof of the parametric representation

The proof of the parametric representation is easily done by using complex numbers and their representation as complex plane. The movement of the small circle can be split into two rotations. In the complex plane a rotation of a point z around point 0 (origin) by an angle φ can be performed by the multiplication of point z (complex number) by e i φ . Hence the

rotation Φ 3 around point 3 a by angle 2 φ is : z ↦ 3 a + ( z − 3 a ) e i 2 φ ,rotation Φ 0 around point 0 by angle φ is : z ↦ z e i φ .

A point p ( φ ) of the nephroid is generated by the rotation of point 2 a by Φ 3 and the subsequent rotation with Φ 0 :

p ( φ ) = Φ 0 ( Φ 3 ( 2 a ) ) = Φ 0 ( 3 a − a e i 2 φ ) = ( 3 a − a e i 2 φ ) e i φ = 3 a e i φ − a e i 3 φ .

Herefrom one gets

x ( φ ) = 3 a cos ⁡ φ − a cos ⁡ 3 φ = 6 a cos ⁡ φ − 4 a cos 3 ⁡ φ   , y ( φ ) = 3 a sin ⁡ φ − a sin ⁡ 3 φ = 4 a sin 3 ⁡ φ .

(The formulae e i φ = cos ⁡ φ + i sin ⁡ φ ,   cos 2 ⁡ φ + sin 2 ⁡ φ = 1 ,   cos ⁡ 3 φ = 4 cos 3 ⁡ φ − 3 cos ⁡ φ , sin ⁡ 3 φ = 3 sin ⁡ φ − 4 sin 3 ⁡ φ were used. See trigonometric functions.)

proof of the implicit representation

With

x 2 + y 2 − 4 a 2 = ( 3 a cos ⁡ φ − a cos ⁡ 3 φ ) 2 + ( 3 a sin ⁡ φ − a sin ⁡ 3 φ ) 2 − 4 a 2 = ⋯ = 6 a 2 ( 1 − cos ⁡ 2 φ ) = 12 a 2 sin 2 ⁡ φ

one gets

( x 2 + y 2 − 4 a 2 ) 3 = ( 12 a 2 ) 3 sin 6 ⁡ φ = 108 a 4 ( 4 a sin 3 ⁡ φ ) 2 = 108 a 4 y 2   .

other orientaion

If the cusps are on the y-axis the parametric representation is

x = 3 a cos ⁡ φ + a cos ⁡ 3 φ , y = 3 a sin ⁡ φ + a sin ⁡ 3 φ ) .

and the implicit one:

( x 2 + y 2 − 4 a 2 ) 3 = 108 a 4 x 2 .

Metric properties

For the nephroid above the

arclength is L = 24 a ,

area A = 12 π a 2   and

radius of curvature is ρ = | 3 a sin ⁡ φ | .

The proofs of these statements use suitable formulae on curves (arc length, area and radius of curvature) and the parametric representation above

x ( φ ) = 6 a cos ⁡ φ − 4 a cos 3 ⁡ φ   , y ( φ ) = 4 a sin 3 ⁡ φ

and their derivatives

x ˙ = − 6 a sin ⁡ φ ( 1 − 2 cos 2 ⁡ φ )   ,   x ¨ = − 6 a cos ⁡ φ ( 5 − 6 cos 2 ⁡ φ )   , y ˙ = 12 a sin 2 ⁡ φ cos ⁡ φ , y ¨ = 12 a sin ⁡ φ ( 3 cos 2 ⁡ φ − 1 )   .

proof for the arc length

L = 2 ∫ 0 π x ˙ 2 + y ˙ 2 d φ = ⋯ = 12 a ∫ 0 π sin ⁡ φ d φ = 24 a .

proof for the area

A = 2 ⋅ 1 2 | ∫ 0 π [ x y ˙ − y x ˙ ] d φ | = ⋯ = 24 a 2 ∫ 0 π sin 2 ⁡ φ d φ = 12 π a 2 .

proof for the radius of curvature

ρ = | ( x ˙ 2 + y ˙ 2 ) 3 2 x ˙ y ¨ − y ˙ x ¨ | = ⋯ = | 3 a sin ⁡ φ | .

Nephroid as envelope of a pencil of circles

Let be c 0 a circle and D 1 , D 2 points of a diameter d 12 , then the envelope of the pencil of circles, which have midpoints on c 0 and are touching d 12 is a nephroid with cusps D 1 , D 2 .

proof

Let c 0 be the circle ( 2 a cos ⁡ φ , 2 a sin ⁡ φ ) with midpoint ( 0 , 0 ) and radius 2 a . The diameter may lie on the x-axis (s. picture). The pencil of circles has equations:

f ( x , y , φ ) = ( x − 2 a cos ⁡ φ ) 2 + ( y − 2 a sin ⁡ φ ) 2 − ( 2 a sin ⁡ φ ) 2 = 0   .

The envelope condition is

f φ ( x , y , φ ) = 2 a ( x sin ⁡ φ − y cos ⁡ φ − 2 a cos ⁡ φ sin ⁡ φ ) = 0   .

One easily checks that the point of the nephroid p ( φ ) = ( 6 a cos ⁡ φ − 4 a cos 3 ⁡ φ , 4 a sin 3 ⁡ φ ) is a solution of the system f ( x , y , φ ) = 0 , f φ ( x , y , φ ) = 0 and hence a point of the envelope of the pencil of circles.

Nephroid as envelope of a pencil of lines

Similar to the generation of a cardioid as envelope of a pencil of lines the following procedure holds:

1. Draw a circle, divide its perimeter into equal spaced parts with 3 N points (s. picture) and number them consecutively.
2. Draw the chords: ( 1 , 3 ) , ( 2 , 6 ) , . . . . , ( n , 3 n ) , . . . . , ( N , 3 N ) , ( N + 1 , 3 ) , ( N + 2 , 6 ) , . . . . , . (i.e.: The second point is moved by threefold velocity.)
3. The envelope of these chords is a nephroid.

proof

The following consideration uses trigonometric formulae for cos ⁡ α + cos ⁡ β ,   sin ⁡ α + sin ⁡ β ,   cos ⁡ ( α + β ) ,   cos ⁡ 2 α . In order to keep the calculations simple, the proof is given for the nephroid with cusps on the y-axis.

equation of the tangent

for the nephroid with parametric representation x = 3 cos ⁡ φ + cos ⁡ 3 φ , y = 3 sin ⁡ φ + sin ⁡ 3 φ :

Herefrom one determines the normal vector n → = ( y ˙ , − x ˙ ) T , at first.
The equation of the tangent y ˙ ( φ ) ⋅ ( x − x ( φ ) ) − x ˙ ( φ ) ⋅ ( y − y ( φ ) ) = 0 is:

( cos ⁡ 2 φ ⋅ x   +   sin ⁡ 2 φ ⋅ y ) cos ⁡ φ = 4 cos 2 ⁡ φ   .

For φ = π 2 , 3 π 2 one gets the cusps of the nephroid, where there is no tangent. For φ ≠ π 2 , 3 π 2 one can divide by cos ⁡ φ and yields at last

cos ⁡ 2 φ ⋅ x + sin ⁡ 2 φ ⋅ y = 4 cos ⁡ φ   .

equation of the chord

to the circle with midpoint ( 0 , 0 ) and radius 4 : The equation of the chord containing the two points ( 4 cos ⁡ θ , 4 sin ⁡ θ ) ,   ( 4 cos ⁡ 3 θ , 4 sin ⁡ 3 θ ) ) is: ( cos ⁡ 2 θ ⋅ x + sin ⁡ 2 θ ⋅ y ) sin ⁡ θ = 4 cos ⁡ θ sin ⁡ θ   .

For θ = 0 , π the chord degenerates to a point. For θ ≠ 0 , π one can divide by sin ⁡ θ and gets the equation of the chord:

cos ⁡ 2 θ ⋅ x + sin ⁡ 2 θ ⋅ y = 4 cos ⁡ θ   .

The two angles φ , θ are defined differently ( φ is one half of the rolling angle, θ is the parameter of the circle, whose chords are determined), for φ = θ one gets the same line. Hence any chord from the circle above is tangent to the nephroid and

the nephroid is the envelope of the chords of the circle.

Nephroid as caustic of one half of a circle

The considerations made in the previous section give a proof for the fact, that the caustic of one half of a circle is a nephroid.

If in the plane parallel light rays meet a reflecting half of a circle (s. picture), then the reflected rays are tangent to a nephroid.

proof

The circle may have the origin as midpoint (as in the previous section) and its radius is 4 . The circle has the parametric representation

k ( φ ) = 4 ( cos ⁡ φ , sin ⁡ φ )   .

The tangent at the circle point K :   k ( φ ) has normal vector n → t = ( cos ⁡ φ , sin ⁡ φ ) T . The reflected ray has the normal vector (s. picture) n → r = ( cos ⁡ 2 φ , sin ⁡ 2 φ ) T and containing circle point K :   4 ( cos ⁡ φ , sin ⁡ φ ) . Hence the reflected ray is part of the line with equation

cos ⁡ 2 φ ⋅ x   +   sin ⁡ 2 φ ⋅ y = 4 cos ⁡ φ   ,

which is tangent to the nephroid of the previous section at point

P :   ( 3 cos ⁡ φ + cos ⁡ 3 φ , 3 sin ⁡ φ + sin ⁡ 3 φ ) (s. above).

evolute

The evolute of a curve is the locus of centers of curvature. In detail: For a curve x → = c → ( s ) with radius of curvature ρ ( s ) the evolute has the representation

x → = c → ( s ) + ρ ( s ) n → ( s ) .

with n → ( s ) the suitably oriented unit normal.

For a nephroide one gets:

The evolute of a nephroid is another nephroid half as large and rotated 90 degrees (s. picture).

proof

The nephroid as shown in the picture has the parametric representation

x = 3 cos ⁡ φ + cos ⁡ 3 φ , y = 3 sin ⁡ φ + sin ⁡ 3 φ   ,

the unit normal vector pointing to the center of curvature

n → ( φ ) = ( − cos ⁡ 2 φ , − sin ⁡ 2 φ ) T (see section above)

and the radius of curvature 3 cos ⁡ φ (s. section on metric properties). Hence the evolute has the representation:

x = 3 cos ⁡ φ + cos ⁡ 3 φ − 3 cos ⁡ φ ⋅ cos ⁡ 2 φ = ⋯ = 3 cos ⁡ φ − 2 cos 3 ⁡ φ , y = 3 sin ⁡ φ + sin ⁡ 3 φ − 3 cos ⁡ φ ⋅ sin ⁡ 2 φ   = ⋯ = 2 sin 3 ⁡ φ   ,

which is a nephroid half as large and rotated 90 degrees (s. picture and section equations above)

involute

Because the evolute of a nephroid is another nephroid, so the involute of the nephroid is also another nephroid. The original nephroid in the image is the involute of the smaller nephroid.

Inversion of a nephroid

The inversion

x ↦ 4 a 2 x x 2 + y 2 , y ↦ 4 a 2 y x 2 + y 2

across the circle with midpoint ( 0 , 0 ) and radius 2 a maps the nephroid with equation

( x 2 + y 2 − 4 a 2 ) 3 = 108 a 4 y 2

onto the curve of degree 6 with equation

( 4 a 2 − ( x 2 + y 2 ) ) 3 = 27 a 2 ( x 2 + y 2 ) y 2 (s. picture) .