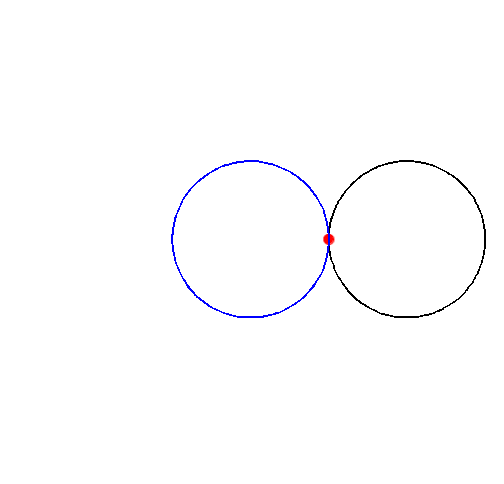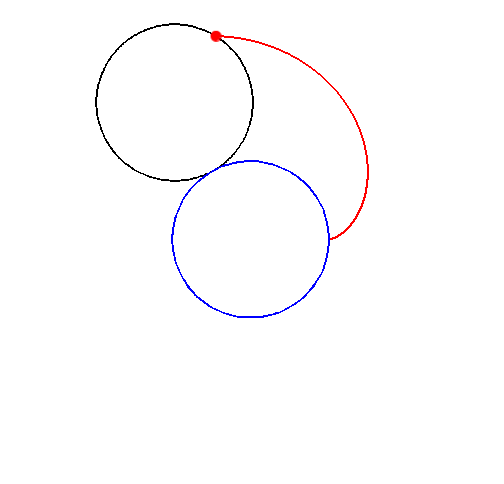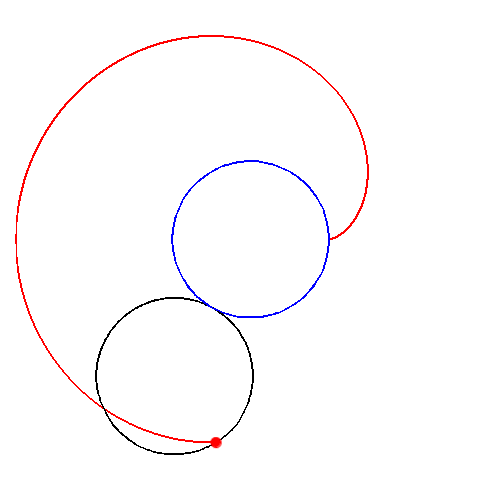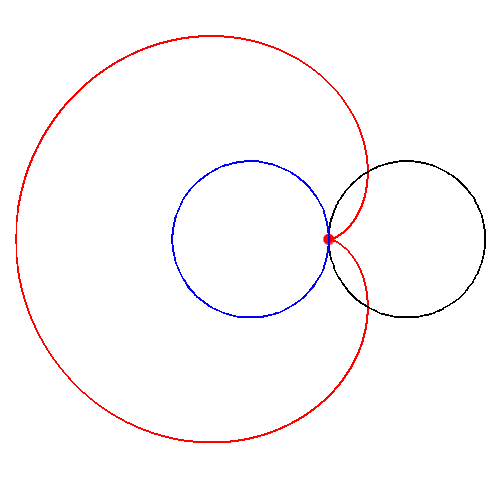
Cardioid - Alchetron, The Free Social Encyclopedia

A cardioid (from the Greek καρδία "heart") is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion.

A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid, (any 2d plane containing the 3d straight line of the microphone body.) In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the "stalk" of the apple.

Equations

Let be a the common radius of the two generating circles with midpoints ( − a , 0 ) , ( a , 0 ) , φ the rolling angle and the origin the starting point (see picture). One gets

the parametric representation:

x ( φ ) = 2 a ( 1 − cos ⁡ φ ) ⋅ cos ⁡ φ , y ( φ ) = 2 a ( 1 − cos ⁡ φ ) ⋅ sin ⁡ φ , 0 ≤ φ < 2 π

and the representation in

the polar coordinates:

r ( φ ) = 2 a ( 1 − cos ⁡ φ ) .

Introducing the substitutions cos ⁡ φ = x / r and r = x 2 + y 2 one gets after removing the square root the implicit representation in

cartesian coordinates:

( x 2 + y 2 ) 2 + 4 a x ( x 2 + y 2 ) − 4 a 2 y 2 = 0 .

proof for the parametric representation

The proof can be done easily using complex numbers and their common describtion as complex plane. The rolling movement of the black circle on the blue one can be split into two rotations. In the complex plane a rotation around point 0 (origin) by an angle φ can be performed by the multiplication of a point z (complex number) by e i φ . Hence the

rotation Φ + around point a is : z ↦ a + ( z − a ) e i φ ,rotation Φ − around point − a is: z ↦ − a + ( z + a ) e i φ .

A point p ( φ ) of the cardiod is generated by rotating the origin around point a and subsequent rotating around − a by the same angle φ :

p ( φ ) = Φ − ( Φ + ( 0 ) ) = Φ − ( a − a e i φ ) = − a + ( a − a e i φ + a ) e i φ = a ( − e i 2 φ + 2 e i φ − 1 ) .

Herefrom one gets the parametric representation above:

x ( φ ) = a ( − cos ⁡ ( 2 φ ) + 2 cos ⁡ φ − 1 ) = 2 a ( 1 − cos ⁡ φ ) ⋅ cos ⁡ φ y ( φ ) = a ( − sin ⁡ ( 2 φ ) + 2 sin ⁡ φ ) = 2 a ( 1 − cos ⁡ φ ) ⋅ sin ⁡ φ .

(The folowing formulas e i φ = cos ⁡ φ + i sin ⁡ φ , ( cos ⁡ φ ) 2 + ( sin ⁡ φ ) 2 = 1 , cos ⁡ 2 φ = ( cos ⁡ φ ) 2 − ( sin ⁡ φ ) 2 , sin ⁡ 2 φ = 2 sin ⁡ φ cos ⁡ φ were used. See trigonometric functions.)

Area and arc length

For the cardiod as defined above the following formulas hold:

area A = 6 π a 2 and

arc length L = 16 a .

The proofs of these statement use in both cases the polar representation of the cardioid. For suitable formulas see polar coordinate system (arc length) and polar coordinate system (area)

proof of the area formular

A = 2 ⋅ 1 2 ∫ 0 π ( r ( φ ) ) 2 d φ = ∫ 0 π 4 a 2 ( 1 − cos ⁡ φ ) 2 d φ = ⋯ = 4 a 2 ⋅ 3 2 π = 6 π a 2 .

proof of the arc length formular

L = 2 ∫ 0 π r ( φ ) 2 + ( r ′ ( φ ) ) 2 d φ = ⋯ = 8 a ∫ 0 π 1 2 ( 1 − cos ⁡ φ ) d φ = 8 a ∫ 0 π sin ⁡ ( φ 2 ) d φ = 16 a .

Inverse curve

The cardioid is one possible inverse curve for a parabola. Specifically, if a parabola is inverted across any circle whose center lies at the focus of the parabola, the result is a cardioid. The cusp of the resulting cardioid will lie at the center of the circle, and corresponds to the vanishing point of the parabola.

In terms of stereographic projection, this says that a parabola in the Euclidean plane is the projection of a cardioid drawn on the sphere whose cusp is at the north pole.

Not every inverse curve of a parabola is a cardioid. For example, if a parabola is inverted across a circle whose center lies at the vertex of the parabola, then the result is a cissoid of Diocles.

The picture to the right shows the parabola with polar equation

ρ ( θ ) = 1 1 − cos ⁡ θ .

In Cartesian coordinates, this is the parabola y 2 = 2 x + 1 . When this parabola is inverted across the unit circle, the result is a cardioid with the reciprocal equation

ρ ( θ ) = 1 − cos ⁡ θ .

Cardioids in different positions

Choosing other positions of the cardioid within the coordinate system results in different equations. The pictutre shows the 4 most common positions of a cardioid and their polar equations.

Cardioids in complex analysis

In complex analysis, the image of any circle through the origin under the map z → z 2 is a cardioid. One application of this result is that the boundary of the central bulb of the Mandelbrot set is a cardioid given by the equation

c = 1 − ( e i t − 1 ) 2 4 .

The Mandelbrot set contains an infinite number of slightly distorted copies of itself and the central bulb of any of these smaller copies is an approximate cardioid.

Caustics

Certain caustics can take the shape of cardioids. The catacaustic of a circle with respect to a point on the circumference is a cardioid. Also, the catacaustic of a cone with respect to rays parallel to a generating line is a surface whose cross section is a cardioid. This can be seen, as in the photograph to the right, in a conical cup partially filled with liquid when a light is shining from a distance and at an angle equal to the angle of the cone. The shape of the curve at the bottom of a cylindrical cup is half of a nephroid, which looks quite similar.

References

Cardioid Wikipedia

(Text) CC BY-SA

Contents