 | ||
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology, algebraic geometry and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'. It is closely associated with covering maps and their degeneration into ramification; the aspect giving rise to monodromy phenomena is that certain functions we may wish to define fail to be single-valued as we 'run round' a path encircling a singularity. The failure of monodromy can be measured by defining a monodromy group: a group of transformations acting on the data that encodes what does happen as we 'run round'.
Contents
Definition
Let X be a connected and locally connected based topological space with base point x, and let
Example
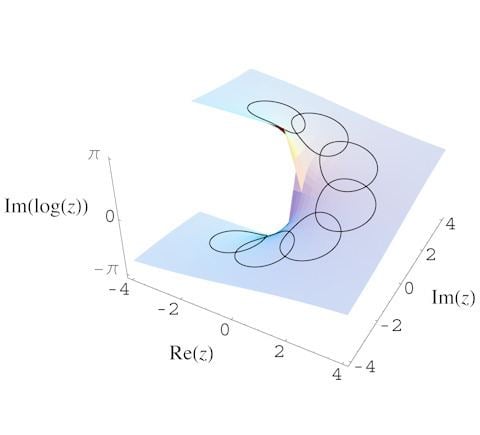
These ideas were first made explicit in complex analysis. In the process of analytic continuation, a function that is an analytic function F(z) in some open subset E of the punctured complex plane C {0} may be continued back into E, but with different values. For example, take
then analytic continuation anti-clockwise round the circle
will result in the return, not to F(z) but
In this case the monodromy group is infinite cyclic and the covering space is the universal cover of the punctured complex plane. This cover can be visualized as the helicoid (as defined in the helicoid article) restricted to ρ > 0. The covering map is a vertical projection, in a sense collapsing the spiral in the obvious way to get a punctured plane.
Differential equations in the complex domain
One important application is to differential equations, where a single solution may give further linearly independent solutions by analytic continuation. Linear differential equations defined in an open, connected set S in the complex plane have a monodromy group, which (more precisely) is a linear representation of the fundamental group of S, summarising all the analytic continuations round loops within S. The inverse problem, of constructing the equation (with regular singularities), given a representation, is called the Riemann–Hilbert problem.
For a regular (and in particular Fuchsian) linear system one usually chooses as generators of the monodromy group the operators Mj corresponding to loops each of which circumvents just one of the poles of the system counterclockwise. If the indices j are chosen in such a way that they increase from 1 to p + 1 when one circumvents the base point clockwise, then the only relation between the generators is the equality
Topological and geometric aspects
In the case of a covering map, we look at it as a special case of a fibration, and use the homotopy lifting property to 'follow' paths on the base space X (we assume it path-connected for simplicity) as they are lifted up into the cover C. If we follow round a loop based at x in X, which we lift to start at c above x, we'll end at some c* again above x; it is quite possible that c ≠ c*, and to code this one considers the action of the fundamental group π1(X, x) as a permutation group on the set of all c, as a monodromy group in this context.
In differential geometry, an analogous role is played by parallel transport. In a principal bundle B over a smooth manifold M, a connection allows 'horizontal' movement from fibers above m in M to adjacent ones. The effect when applied to loops based at m is to define a holonomy group of translations of the fiber at m; if the structure group of B is G, it is a subgroup of G that measures the deviation of B from the product bundle M × G.
Monodromy groupoid and foliations
Analogous to the fundamental groupoid it is possible to get rid of the choice of a base point and to define a monodromy groupoid. Here we consider (homotopy classes of) lifts of paths in the base space X of a fibration
Moreover the construction can also be generalized to foliations: Consider
Definition via Galois theory
Let F(x) denote the field of the rational functions in the variable x over the field F, which is the field of fractions of the polynomial ring F[x]. An element y = f(x) of F(x) determines a finite field extension [F(x) : F(y)].
This extension is generally not Galois but has Galois closure L(f). The associated Galois group of the extension [L(f) : F(y)] is called the monodromy group of f.
In the case of F = C Riemann surface theory enters and allows for the geometric interpretation given above. In the case that the extension [C(x) : C(y)] is already Galois, the associated monodromy group is sometimes called a group of deck transformations.
This has connections with the Galois theory of covering spaces leading to the Riemann existence theorem.
