Misiurewicz point - Alchetron, The Free Social Encyclopedia

In mathematics, a Misiurewicz point is a parameter in the Mandelbrot set (the parameter space of quadratic polynomials) for which the critical point is strictly preperiodic (i.e., it becomes periodic after finitely many iterations but is not periodic itself). By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic. (This term makes less sense for maps in greater generality that have more than one (free) critical point because some critical points might be periodic and others not.)

Mathematical notation

A parameter c is a Misiurewicz point M k , n if it satisfies the equations

f c ( k ) ( z c r ) = f c ( k + n ) ( z c r )

and

f c ( k − 1 ) ( z c r ) ≠ f c ( k + n − 1 ) ( z c r )

so :

M k , n = c : f c ( k ) ( z c r ) = f c ( k + n ) ( z c r )

where :

z c r is a critical point of f c ,

k and n are positive integers,

f c k denotes the k -th iterate of f c .

Name

Misiurewicz points are named after the Polish-American mathematician Michał Misiurewicz.

Note that the term "Misiurewicz point" is used ambiguously: Misiurewicz originally investigated maps in which all critical points were non-recurrent (that is, there is a neighborhood of every critical point that is not visited by the orbit of this critical point), and this meaning is firmly established in the context of dynamics of iterated interval maps. The case that for a quadratic polynomial the unique critical point is strictly preperiodic is only a very special case; in this restricted sense (as described above) this term is used in complex dynamics; a more appropriate term would be Misiurewicz-Thurston points (after William Thurston who investigated postcritically finite rational maps).

Synonyms

hub ( in case of branch point)

Quadratic maps

A complex quadratic polynomial has only one critical point. By a suitable conjugation any quadratic polynomial can be transformed into a map of the form P c ( z ) = z 2 + c which has a single critical point at z = 0 . The Misiurewicz points of this family of maps are roots of the equations

P c ( k ) ( 0 ) = P c ( k + n ) ( 0 ) ,

(subject to the condition that the critical point is not periodic), where :

k is the pre-period

n is the period

P c ( n ) = P c ( P c ( n − 1 ) ) denotes the n-fold composition of P c ( z ) = z 2 + c with itself i.e. the n^th iteration of P c .

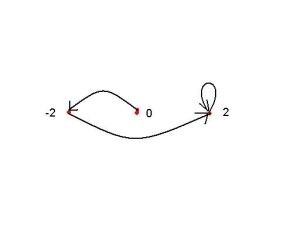
For example, the Misiurewicz points with k=2 and n=1, denoted by M_2,1, are roots of

P c ( 2 ) ( 0 ) = P c ( 3 ) ( 0 ) ⇒ c 2 + c = ( c 2 + c ) 2 + c ⇒ c 4 + 2 c 3 = 0 .

The root c=0 is not a Misiurewicz point because the critical point is a fixed point when c=0, and so is periodic rather than pre-periodic. This leaves a single Misiurewicz point M_2,1 at c = −2.

Properties of Misiurewicz points of complex quadratic mapping

Misiurewicz points belong to the boundary of the Mandelbrot set. Misiurewicz points are dense in the boundary of the Mandelbrot set.

If c is a Misiurewicz point, then the associated filled Julia set is equal to the Julia set, and means the filled Julia set has no interior.

If c is a Misiurewicz point, then in the corresponding Julia set all periodic cycles are repelling (in particular the cycle that the critical orbit falls onto).

Mandelbrot set and Julia set J c are locally asymptotically similar around Misiurewicz points. Mandelbrot set is self-similar around Misiurewicz points

Types

Misiurewicz points can be classified according to number of external rays that land on them :, points where branches meet

branch points ( = points that disconnect the Mandelbrot set into at least three components.) with 3 or more external arguments ( angles )

non-branch points with exactly 2 external arguments ( = interior points of arcs within the Mandelbrot set) : these points are less conspicuous and thus not so easily to find on pictures.

end points with 1 external argument ( branch tips )

According to the Branch Theorem of the Mandelbrot set, all branch points of the Mandelbrot set are Misiurewicz points (plus, in a combinatorial sense, hyperbolic components represented by their centers).

Many (actually, most) Misiurewicz parameters in the Mandelbrot set look like `centers of spirals'. The explanation for this is the following: at a Misiurewicz parameter, the critical value jumps onto a repelling periodic cycle after finitely many iterations; at each point on the cycle, the Julia set is asymptotically self-similar by a complex multiplication by the derivative of this cycle. If the derivative is non-real, then this implies that the Julia set, near the periodic cycle, has a spiral structure. A similar spiral structure thus occurs in the Julia set near the critical value and, by Tan Lei's aforementioned theorem, also in the Mandelbrot set near any Misiurewicz parameter for which the repelling orbit has non-real multiplier. Depending on the value of the multiplier, the spiral shape can seem more or less pronounced. The number of the arms at the spiral equals the number of branches at the Misiurewicz parameter, and this equals the number of branches at the critical value in the Julia set. (Even the `principal Misiurewicz point in the 1/3-limb', at the end of the parameter rays at angles 9/56, 11/56, and 15/56, turns out to be asymptotically a spiral, with infinitely many turns, even though this is hard to see without maginification.)

External arguments

External arguments of Misiurewicz points, measured in turns are :

where: a and b are positive integers and b is odd, subscript number shows base of numeral system.

End points

Point c = M 2 , 2 = i :

is a tip of the filament

Its critical orbits is { 0 , i , i − 1 , − i , i − 1 , − i . . . }

Point c = M 2 , 1 = − 2

is the end-point of main antenna of Mandelbrot set

Its critical orbits is { 0 , − 2 , 2 , 2 , 2 , . . . }

Symbolic sequence = C L R R R ...

preperiod is 2 and period 1

Notice that it is z-plane (dynamical plane) not c-plane (parameter plane) and point z = − 2 is not the same point as c = − 2 .

Point c = − 2 = M 2 , 1 is landing point of only one external ray ( parameter ray) of angle 1/2 .

Non-Branch points

Point c = − 0.77568377 + 0.13646737 ∗ i is near a Misiurewicz point M 23 , 2 . It is

a center of a two-arms spiral

a landing point of 2 external rays with angles : 8388611 25165824 and 8388613 25165824 where denominator is 3 ∗ 2 23

preperiodic point with preperiod k = 23 and period n = 2

Point c = − 1.54368901269109 is near a Misiurewicz point M 3 , 1 ,

which is landing point for pair of rays : 5 12 , 7 12

has preperiod k = 3 and period n = 1

Point c = − 0.1010... + 0.9562... ∗ i = M 4 , 1 is a principal Misiurewicz point of the 1/3 limb. It has 3 external rays 9/56, 11/56 and 15/56.

References

Misiurewicz point Wikipedia

(Text) CC BY-SA

Contents