 | ||
In mathematics, specifically in topology, the interior of a subset S of points of a topological space X consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S.
Contents
- Interior point
- Interior of a set
- Examples
- Interior operator
- Exterior of a set
- Interior disjoint shapes
- References
The interior of S is the complement of the closure of the complement of S. In this sense interior and closure are dual notions.
The exterior of a set is the interior of its complement, equivalently the complement of its closure; it consists of the points that are in neither the set nor its boundary. The interior, boundary, and exterior of a subset together partition the whole space into three blocks (or fewer when one or more of these is empty). The interior and exterior are always open while the boundary is always closed. Sets with empty interior have been called boundary sets.
Interior point
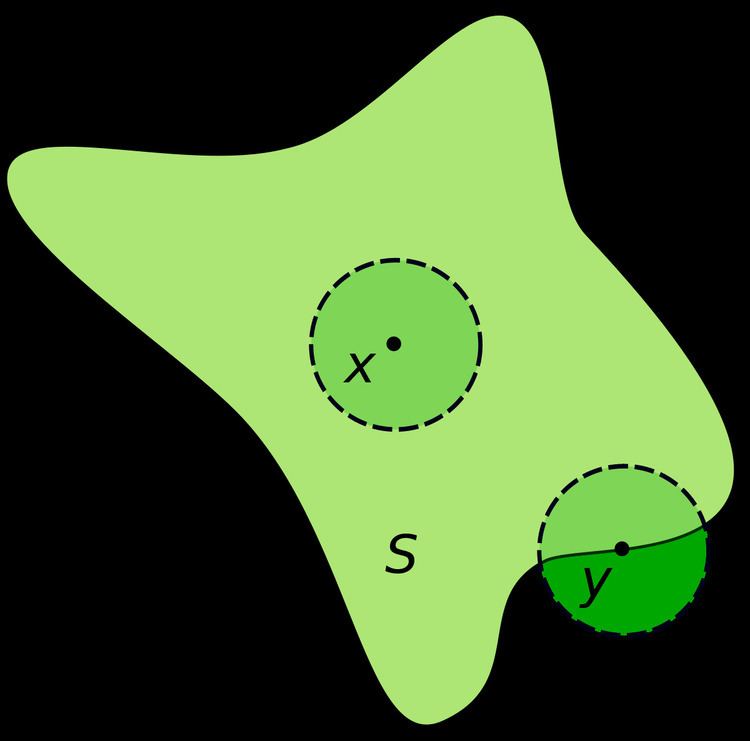
If S is a subset of a Euclidean space, then x is an interior point of S if there exists an open ball centered at x which is completely contained in S. (This is illustrated in the introductory section to this article.)
This definition generalizes to any subset S of a metric space X with metric d: x is an interior point of S if there exists r > 0, such that y is in S whenever the distance d(x, y) < r.
This definition generalises to topological spaces by replacing "open ball" with "open set". Let S be a subset of a topological space X. Then x is an interior point of S if x is contained in an open subset of S. (Equivalently, x is an interior point of S if there exists a neighbourhood of x which is contained in S.)
Interior of a set
The interior of a set S is the set of all interior points of S. The interior of S is denoted int(S), Int(S) or So. The interior of a set has the following properties.
Sometimes the second or third property above is taken as the definition of the topological interior.
Note that these properties are also satisfied if "interior", "subset", "union", "contained in", "largest" and "open" are replaced by "closure", "superset", "intersection", "which contains", "smallest", and "closed", respectively. For more on this matter, see interior operator below.
Examples
On the set of real numbers one can put other topologies rather than the standard one.
These examples show that the interior of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.
Interior operator
The interior operator o is dual to the closure operator —, in the sense that
and also
where X is the topological space containing S, and the backslash refers to the set-theoretic difference.
Therefore, the abstract theory of closure operators and the Kuratowski closure axioms can be easily translated into the language of interior operators, by replacing sets with their complements.
Exterior of a set
The exterior of a subset S of a topological space X, denoted ext(S) or Ext(S), is the interior int(X \ S) of its relative complement. Alternatively, it can be defined as X \ S—, the complement of the closure of S. Many properties follow in a straightforward way from those of the interior operator, such as the following.
Unlike the interior operator, ext is not idempotent, but the following holds:
Interior-disjoint shapes
Two shapes a and b are called interior-disjoint if the intersection of their interiors is empty. Interior-disjoint shapes may or may not intersect in their boundary.
