Matrix representation of conic sections

Classification

Proper (non-degenerate) and degenerate conic sections can be distinguished based on the determinant of A_Q.

If det A Q = 0 , the conic is degenerate.

If det A Q ≠ 0 so that Q is not degenerate, we can see what type of conic section it is by computing the minor, det A 33 :

In the case of an ellipse, we can distinguish the special case of a circle by comparing the last two diagonal elements corresponding to the coefficients of x² and y²:

Moreover, in the case of a non-degenerate ellipse (with det A 33 > 0 and det A Q ≠ 0 ), we have a real ellipse if ( A + C ) det A Q < 0 but an imaginary ellipse if ( A + C ) det A Q > 0 . An example of the latter is x 2 + y 2 + 10 = 0 , which has no real-valued solutions.

If the conic section is degenerate ( det A Q = 0 ), det A 33 still allows us to distinguish its form:

The case of coincident lines occurs if and only if the rank of the 3×3 matrix A Q is 1; in all other degenerate cases its rank is 2.

Central conics

When det A 33 ≠ 0 a geometric center of the conic section exists and such conic sections (ellipses and hyperbolas) are called central conics.

Center

The center of a conic, if it exists, is a point that bisects all the chords of the conic that pass through it. This property can be used to calculate the coordinates of the center, which can be shown to be the point where the gradient of the quadratic function Q vanishes—that is,

This yields the center as given below.

An alternative approach that uses the matrix form of the quadratic equation is based on the fact that when the center is the origin of the coordinate system, there are no linear terms in the equation. Any translation to a coordinate origin (x₀, y₀), using x*= x – x₀, y* = y – y₀ gives rise to

The condition for (x₀, y₀) to be the conic's center (x_c, y_c) is that the coefficients of the linear x* and y* terms, when this equation is multiplied out, are zero. This condition produces the coordinates of the center:

This calculation can also be accomplished by taking the first two rows of the associated matrix A_Q, multiplying each by (x, y, 1)^⊤ and setting both inner products equal to 0, obtaining the following system:

This yields the above center point.

In the case of a parabola, that is, when 4AC − B² = 0, there is no center since the above denominators become zero (or, interpreted projectively, the center is on the line at infinity.)

Centered matrix equation

A central (non-parabola) conic A x 2 + B x y + C y 2 + D x + E y + F = 0 can be rewritten in centered matrix form as

where

Then for the ellipse case of AC > (B/2)², the ellipse is real if the sign of K equals the sign of (A + C) (that is, the sign of each of A and C), imaginary if they have opposite signs, and a degenerate point ellipse if K = 0. In the hyperbola case of AC < (B/2)², the hyperbola is degenerate if and only if K = 0.

Standard form of a central conic

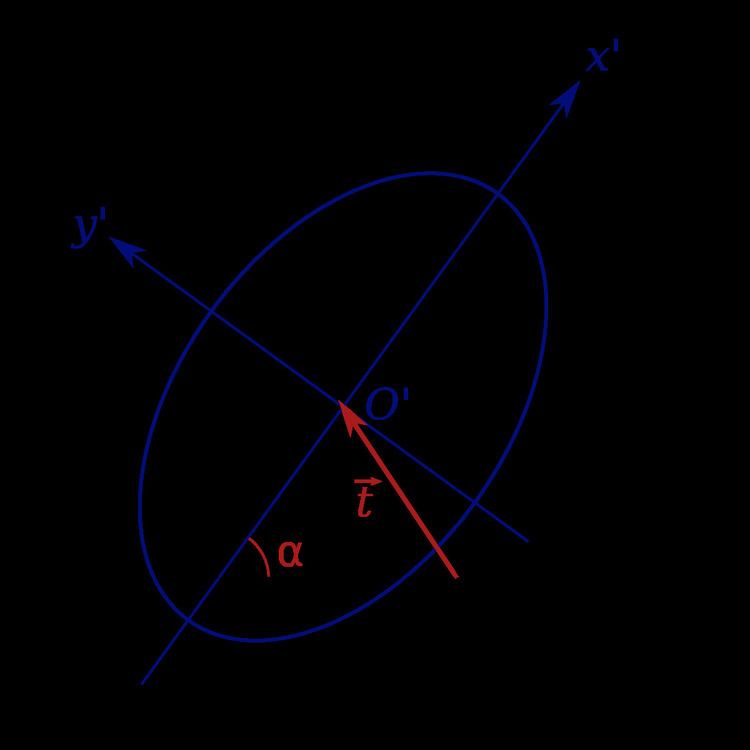
The standard form of the equation of a central conic section is obtained when the conic section is translated and rotated so that its center lies at the center of the coordinate system and its axes coincide with the coordinate axes. This is equivalent to saying that the coordinate system's center is moved and the coordinate axes are rotated to satisfy these properties. In the diagram, the original xy-coordinate system with origin O is moved to the x'y'-coordinate system with origin O'.

The translation is by the vector t → = ( x c y c ) .

The rotation by angle α can be carried out by diagonalizing the matrix A₃₃. Thus, if λ 1 and λ 2 are the eigenvalues of the matrix A₃₃, the centered equation can be rewritten in new variables x' and y' as

Dividing by K = − det A Q det A 33 we obtain a standard canonical form.

For example, for an ellipse this form is

From here we get a and b, the lengths of the semi-major and semi-minor axes in conventional notation.

For central conics, both eigenvalues are non-zero and the classification of the conic sections can be obtained by examining them.

Axes

By the principal axis theorem, the two eigenvectors of the matrix of the quadratic form of a central conic section (ellipse or hyperbola) are perpendicular (orthogonal to each other) and each is parallel to (in the same direction as) either the major or minor axis of the conic. The eigenvector having the smallest eigenvalue (in absolute value) corresponds to the major axis.

Specifically, if a central conic section has center (x_c, y_c) and an eigenvector of A₃₃ is given by v→(v₁, v₂) then the principal axis (major or minor) corresponding to that eigenvector has equation,

Vertices

The vertices of a central conic can be determined by calculating the intersections of the conic and its axes — in other words, by solving the system consisting of the quadratic conic equation and the linear equation for alternately one or the other of the axes. Two or no vertices are obtained for each axis, since, in the case of the hyperbola, the minor axis does not intersect the hyperbola at a point with real coordinates. However, from the broader view of the complex plane, the minor axis of an hyperbola does intersect the hyperbola, but at points with complex coordinates.

Poles and polars

Using homogeneous coordinates, the points

are conjugate with respect to the conic Q provided

The conjugates of a fixed point p either form a line or consist of all the points in the plane of the conic. When the conjugates of p form a line, the line is called the polar of p and the point p is called the pole of the line, with respect to the conic. This relationship between points and lines is called a polarity.

If the conic is non-degenerate, the conjugates of a point always form a line and the polarity defined by the conic is a bijection between the points and lines of the extended plane containing the conic (that is, the plane together with the points and line at infinity).

If the point p lies on the conic Q, the polar line of p is the tangent line to Q at p.

The equation, in homogeneous coordinates, of the polar line of the point p with respect to the non-degenerate conic Q is given by

Just as p uniquely determines its polar line (with respect to a given conic), so each line determines a unique pole p. Furthermore, a point p is on a line L which is the polar of a point r, if and only if the polar of p passes through the point r (La Hire's theorem). Thus, this relationship is an expression of geometric duality between points and lines in the plane.

Several familiar concepts concerning conic sections are directly related to this polarity. The center of a non-degenerate conic can be identified as the pole of the line at infinity. A parabola, being tangent to the line at infinity, would have its center being a point on the line at infinity. Hyperbolas intersect the line at infinity in two distinct points and the polar lines of these points are the asymptotes of the hyperbola and are the tangent lines to the hyperbola at these points of infinity. Also, the polar line of a focus of the conic is its corresponding directrix.

Tangents

Let line L be the polar line of point p with respect to the non-degenerate conic Q. By La Hire's theorem, every line passing through p has its pole on L. If L intersects Q in two points (the maximum possible) then the polars of those points are tangent lines that pass through p and such a point is called an exterior or outer point of Q. If L intersects Q in only one point, then it is a tangent line and p is the point of tangency. Finally, if L does not intersect Q then p has no tangent lines passing through it and it is called an interior or inner point.

The equation of the tangent line (in homogeneous coordinates) at a point p on the non-degenerate conic Q is given by,

If p is an exterior point, first find the equation of its polar (the above equation) and then the intersections of that line with the conic, say at points s and t. The polars of s and t will be the tangents through p.

Using the theory of poles and polars, the problem of finding the four mutual tangents of two conics reduces to finding the intersection of two conics.