Lie superalgebra - Alchetron, The Free Social Encyclopedia

In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z₂-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions (but this is not always true; for example, the BRST supersymmetry is the other way around).

Definition

Formally, a Lie superalgebra is a (nonassociative) Z₂-graded algebra, or superalgebra, over a commutative ring (typically R or C) whose product [·, ·], called the Lie superbracket or supercommutator, satisfies the two conditions (analogs of the usual Lie algebra axioms, with grading):

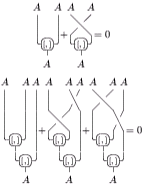
Super skew-symmetry:

[ x , y ] = − ( − 1 ) | x | | y | [ y , x ] .

The super Jacobi identity:

( − 1 ) | x | | z | [ x , [ y , z ] ] + ( − 1 ) | y | | x | [ y , [ z , x ] ] + ( − 1 ) | z | | y | [ z , [ x , y ] ] = 0 ,

where x, y, and z are pure in the Z₂-grading. Here, |x| denotes the degree of x (either 0 or 1). The degree of [x,y] is the sum of degree of x and y modulo 2.

One also sometimes adds the axioms [ x , x ] = 0 for |x| = 0 (if 2 is invertible this follows automatically) and [ [ x , x ] , x ] = 0 for |x| = 1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the Poincaré–Birkhoff–Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold).

Just as for Lie algebras, the universal enveloping algebra of the Lie superalgebra can be given a Hopf algebra structure.

A graded Lie algebra (say, graded by Z or N) that is anticommutative and Jacobi in the graded sense also has a Z 2 grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.

Properties

Let g = g 0 ⊕ g 1 be Lie superalgebra. By inspecting the Jacobi identity, one sees that there are eight cases depending on whether arguments are even or odd. These fall into four classes, indexed by the number of odd elements:

No odd elements. The statement is just that g 0 is an ordinary Lie algebra.
One odd element. Then g 1 is a g 0 -module for the action a d a : b → [ a , b ] , a ∈ g 0 , b , [ a , b ] ∈ g 1 .
Two odd elements. The Jacobi identity says that the bracket g 1 ⊗ g 1 → g 0 is a symmetric g 1 -map.
Three odd elements. For all b ∈ g 1 , [ b , [ b , b ] ] = 0 .

Thus the even subalgebra g 0 of a Lie superalgebra forms a (normal) Lie algebra as all the signs disappear, and the superbracket becomes a normal Lie bracket, while g 1 is a linear representation of g 0 , and there exists a symmetric g 0 -equivariant linear map { ⋅ , ⋅ } : g 1 ⊗ g 1 → g 0 such that,

[ { x , y } , z ] + [ { y , z } , x ] + [ { z , x } , y ] = 0 , x , y , z ∈ g 1 .

Conditions (1)–(3) are linear and can all be understood in terms or ordinary Lie algebras. Condition (4) is nonlinear, and is the most difficult one to verify when constructing a Lie superalgebra starting from an ordinary Lie algebra ( g 0 ) and a representation ( g 1 ).

Involution

A ^∗ Lie superalgebra is a complex Lie superalgebra equipped with an involutive antilinear map from itself to itself which respects the Z₂ grading and satisfies [x,y]^* = [y^*,x^*] for all x and y in the Lie superalgebra. (Some authors prefer the convention [x,y]^* = (−1)^|x||y|[y^*,x^*]; changing * to −* switches between the two conventions.) Its universal enveloping algebra would be an ordinary ^*-algebra.

Examples

Given any associative superalgebra A one can define the supercommutator on homogeneous elements by

[ x , y ] = x y − ( − 1 ) | x | | y | y x

and then extending by linearity to all elements. The algebra A together with the supercommutator then becomes a Lie superalgebra. The simplest example of this procedure is perhaps when A is the space of all linear functions E n d ( V ) of a super vector space V to itself. When V = K p | q , this space is denoted by M p | q or M ( p | q ) . With the Lie bracket per above, the space is denoted g l ( p | q ) .

The Whitehead product on homotopy groups gives many examples of Lie superalgebras over the integers.

Classification

The simple complex finite-dimensional Lie superalgebras were classified by Victor Kac.

The basic classical compact Lie superalgebras (that are not Lie algebras) are: [1]

SU(m/n) These are the superunitary Lie algebras which have invariants:

z . z ¯ + i w . w ¯

This gives two orthosymplectic (see below) invariants if we take the m z variables and n w variables to be non-commutative and we take the real and imaginary parts. Therefore, we have

S U ( m / n ) = O S p ( 2 m / 2 n ) ∩ O S p ( 2 n / 2 m )

SU(n/n)/U(1) A special case of the superunitary Lie algebras where we remove one U(1) generator to make the algebra simple.

OSp(m/2n) These are the Orthosymplectic groups. They have invariants given by:

x . x + y . z − z . y

for m commutative variables (x) and n pairs of anti-commutative variables (y,z). They are important symmetries in supergravity theories.

D(2/1; α ) This is a set of superalgebras parameterised by the variable α . It has dimension 17 and is a sub-algebra of OSp(9|8). The even part of the group is O(3)×O(3)×O(3). So the invariants are:

A μ A μ + B μ B μ + C μ C μ + ψ α β γ ψ α ′ β ′ γ ′ ε α α ′ ε β β ′ ε γ γ ′ A { 1 A 2 A 3 } + B { 1 B 2 B 3 } + C { 1 C 2 C 3 } + A μ Γ μ α α ′ ψ ψ + B μ Γ μ β β ′ ψ ψ + C μ Γ μ γ γ ′ ψ ψ

for particular constants γ .

F(4) This exceptional Lie superalgebra has dimension 40 and is a sub-algebra of OSp(24|16). The even part of the group is O(3)xSO(7) so three invariants are:

B μ ν + B ν μ = 0 A μ A μ + B μ ν B μ ν + ψ { 1 α ψ 2 } α A { 1 A 2 A 3 } + B { μ ν B ν τ B τ μ } + B μ ν σ μ ν α β ψ k α ψ k β + A μ Γ μ α β ψ α k ψ β k + ( sym. )

This group is related to the octonions by considering the 16 component spinors as two component octonion spinors and the gamma matrices acting on the upper indices as unit octonions. We then have f μ ν τ σ ν τ ≡ γ μ where f is the structure constants of octonion multiplication.

G(3) This exceptional Lie superalgebra has dimension 31 and is a sub-algebra of OSp(17|14). The even part of the group is O(3)×G2. The invariants are similar to the above (it being a subalgebra of the F(4)?) so the first invariant is:

A μ A μ + C α μ C α μ + ψ { 1 μ ψ 2 } ν

There are also two so-called strange series called p(n) and q(n).

Classification of infinite-dimensional simple linearly compact Lie superalgebras

The classification consists of the 10 series W(m, n), S(m, n) ((m, n) ≠ (1, 1)), H(2m, n), K(2m + 1, n), HO(m, m) (m ≥ 2), SHO(m, m) (m ≥ 3), KO(m, m + 1), SKO(m, m + 1; β) (m ≥ 2), SHO ∼ (2m, 2m), SKO ∼ (2m + 1, 2m + 3) and the five exceptional algebras:

The last two are particularly interesting (according to Kac) because they have the standard model gauge group SU(3)×SU(2)×U(1) as their zero level algebra. Infinite-dimensional (affine) Lie superalgebras are important symmetries in superstring theory.

Category-theoretic definition

In category theory, a Lie superalgebra can be defined as a nonassociative superalgebra whose product satisfies

[ ⋅ , ⋅ ] ∘ ( id + τ A , A ) = 0

[ ⋅ , ⋅ ] ∘ ( [ ⋅ , ⋅ ] ⊗ id ∘ ( id + σ + σ 2 ) = 0

where σ is the cyclic permutation braiding ( id ⊗ τ A , A ) ∘ ( τ A , A ⊗ id ) . In diagrammatic form:

References

Lie superalgebra Wikipedia

(Text) CC BY-SA

Contents